排行榜
之前的算法都需要数据,但是对于一个新用户,什么数据都没有的情况下,推荐系统对其一无所知,这时候,可以用排行榜来解决这个问题。
排行榜的好处:
- 可以作为解决新用户冷启动问题的推荐策略。当新用户注册时,可以把最近产品中热门的物品推荐给他
- 排行榜可以作为老用户的兴趣发现方式,用户查看个性化推荐的行为,浏览和不浏览商品,都可以作为补充或者更新用户兴趣的数据来源
- 排行榜本身就是一个降级的推荐系统。推荐系统可能出问题,因此排行榜的存在可以作为一种兜底策略,可以避免推荐位开天窗、
排行榜算法
最简单的排行榜,就是直接统计某种指标,按照大小去排序。在社交网站上,按照点赞数、转发数、评论数去排序,在电商网站上按照销量去排序,这是一种最常见、最朴素的排行榜。
这种排行榜简单,容易上线运行,但是有弊端:
- 非常容易被攻击,也就是被刷榜
- 马太效应一直存在,除非强制替换,否则一些破了记录的物品会一直在榜单中
- 不能反映出排行榜随着时间的变化,这一点和马太效应有关
这些弊端的存在,可以改进的措施如下:
考虑时间因素
将排行榜中的物品,看着有一定温度或者重力属性,将如果用户点赞、购买、收藏等行为看成是在投票,如果投票不及时,排行榜上的物品就会掉下来。将该规律反应到排行榜分数的计算规则中,就比简单统计数量要好,再强制按照天更新要科学得多。
Hacker News
Hacker News计算帖子的热度就用到了这个思想,他们统计热度的公式为:
$$ Score = \frac{P -1} {(T + 2)^G} $$
公式中: 1. P: 得票数,去掉帖子作者自己投票 2. T:帖子距离现在的小时数,加上帖子发布到被转帖至Hacker News的平均时长 3. G: 帖子热度的重力因子,其值大小根据情况而定,重力因子越大,帖子的热度衰减越快
分子是简单的帖子数统计,一个小技巧是去掉了作者自己的投票。分母是将时间考虑在内,随着帖子的发表时间增加,分母会逐渐增大,帖子的热门分数会逐渐降低。
牛顿冷却定律
物品受关注度如同温度一样,不输入能量的话它会自然冷却,而且物体的冷却速度和其当前温度与环境温度之差成正比,公式如下:
$$ T(t) = H + Ce^{- \alpha t} $$
公式中字母的意义如下:
- H: 为环境维度,可以认为是平均票数,比如电商中的平均销量,由于不影响排序,可以不适用
- C: 为净剩票数,即时刻t物品已经得到的票数,如物品的销量
- t: 为物品存在时间,一把以小时为单位
- alpha: 是冷却系数,反应物品自然冷却的快慢
alpha的确定可以通过假定经过B个单位后,一个物品增加了A个投票数,但是保持了热门程度不变,则有方程:
$$ Ce^{- \alpha t} = (C + A) e^{- \alpha (t+B)} $$
可以解得:
$$ \alpha = \frac{1} {B} \ln {1+\frac{A}{C}} $$
通过假定A和B的大小,可以获得对应的alpha值。
考虑三种投票
前面的热度计算方法,只考虑用户投票和用户弃权两种,对于有赞成和反对票的情形,一般这样考虑:
- 同样多的总票数,支持赞成票多的,因为这符合平台的长期利益
- 同样多的赞成票数,支持最有价值的,同样则符合平台的长期利益
考虑好评的平均程度
以好评比例作为核心来计算排行榜分数,一个经典的好评率估算公式,叫做威尔逊区间,它考虑了评价的样本数,样本不足时,置信区间很宽,样本很足时,置信区间很窄。这个统计量的应用场景:
- 多大比例的人们会采取某种行为?
- 多大比例的人认为这是一个Spam?
- 多大比例的人认为这是一个“值得推荐的”物品呢?
为每一个物品都计算一个威尔逊区间后,可以采用前面提到的Bandit算法,类UCB的方式取出物品,构建成一个略带变化的排行榜。
电影点评网站为电影排行榜计算分数的公式,针对评分类型数据的排行榜,也叫做贝叶斯平均,如下:
$$ \frac{v}{v+m}R + \frac{m}{v+m}C $$
- R: 物品的平均得分
- v: 参与为这个物品评分的人数
- m: 全局平均每个物品的评分人数
- C: 全局平均每个物品的平均得分
这个公式融合了两个思想:
- 如果物品没多少人为它投票,也就是评价人数不足,那么v就很小,m就很大,公式左边就很小,右边就很大,于是总分算出来很接近右边部分,也就是接近全局平均分C
- 如果物品投票人数多,那么v很大,m很小,分数就接近它自己的平均分R
这个评分的好处是所有的物品,无论有多少人给它评分,都可以统一地计算出一个合理的平均分数。
应对水军刷榜问题
- 单位时间的有效单个物品评论数不能偏离整个网站物品新发布之后同期的评论数太多
- 评分高峰期之后随时间的衰减幅度不能太快
- 参与评分的用户之前长期评分的数量(单位时间多次评分只算一次)越多,对权重的影响越大
- 考虑用户对物品评分和用户自己评分均值的差距
- 考虑评分地址的IP地址,其他设备标识符是否重复,是否有效身份标识,是否有效付费(这部分用户如果比例太低会被作弊者利用)
实用的加权采样算法
在给用户计算出兴趣标签后,每次召回时并不使用全部用户标签,而是按照权重采样一部分标签来使用,这样做的好处:
- 大大减少召回时的计算复杂度
- 可以保留更多的用户标签
- 每次召回计算时还能有所变化
- 虽然有变化,但是还是受到标签的权重相对大小约束
有限数据集
针对有限数据集,采样之前需要遍历一遍所有样本,为每个样本计算一个分数,排序之后选择最高的K个作为样本输出。
假设用户标签若干,每个标签都有权重W,权重高低反映了用户对这个标签的感兴趣程度高低。希望每次输出一部分标签用于召回推荐候选集,每次输出时都不一样,但是又能反应用户标签的权重,输出概率与权重成正比。
这样,需要一个公式:
$$ S_i = R^{\frac{1}{w_i}} $$
公式中:
- W_i是每个样本的权重,比如用户标签的权重
- R是遍历每个样本时产生的0到1之间的随机数
- S_i就是每个样本的采样分数
遍历之后,按照采样分数排序,输出前K个样本就是得到的采样结果。
还有一种加权采样方法是利用指数分布。
无限数据集
上面的方法是针对有限数据集的,每次采样需要遍历所有的样本,对于无限数据集的样本显然是不切实际的。
蓄水池采样
在推荐系统中,针对无限数据集,可以使用蓄水池采样,可以将它使用在:
- 模型融合之后,或者在召回阶段加一层蓄水池采样,这样在不影响整个推荐流程和转化概率的前提下,降低计算复杂度和提升推荐多样性
- 在线阶段要使用用户的反馈行为做实时推荐,对于不同的用户,活跃程度不同,产生的反馈行为数量不同,也可以使用蓄水池采样,为每个用户取出固定数量的行为用于更新推荐结果
假如有一个数据集合,一共有N条,要从中采样取出K个,那么每个样本被选中的概率就是K/N,蓄水池采样的过程:
- 直接去取出K个样本留着,这K个就是随时准备最终要输出的
- 从第K+1个开始,每个都以K/N的概率去替换那留着的K个样本中的一个
在整个过程中,随时可以取出那K个集合作为输出结果。蓄水池采样,顾名思义,K个元素的样本集合就是个蓄水池,是任意时刻的采样结果,可以随时取用。
加权蓄水池采样
加权蓄水池采样结合了加权采样的方法和蓄水池采样的思想,过程如下:
- 为每一个样本生成一个分数,分数还是使用上面的公式S_i计算公式
- 如果结果不足K个,直接保存到结果中
- 如果结果中已经有K个了,如果S_i比已有的结果里最小的那个分数大,就替换它
加权采样的思想就是利用权重影响采样概率。
推荐蓄水池的去重策略
去重是刚需,需要在两个地方去重:
内容源去重
- 对内容做重复检测,直观的思路是分词,然后提取关键词,再两两计算词向量之间的距离,距离小于一定阈值之后就判定为重复。但是对于几千万以上的内容来说就是灾难。
- 使用Simhash
不重复给用户推荐
- 在内容阅读类推荐场景下,给用户推荐的内容不要重复,推荐过的内容就不再出现在推荐候选集中。
- 使用布隆过滤器
对内容源的去重和推荐去重都借助了哈希函数,Simhash是用来加权,Bloomfilter是用来做寻址。
内容源去重:Simhash
只是检测绝对重复,一模一样的情况,直接使用MD5等信息指纹的方法就非常高效。无需再去分词、提取关键词和计算关键词之间的距离。坏处是原始内容改变一个字,就会改变其信息指纹。
Simhash核心思想也是为每个内容生成一个整数表示的指纹,然后用这个指纹去做重复或者相似的检测。过程如下:
- 首先,对原始内容分词,并且计算每个分词的权重
- 对每个词哈希成一个整数,并且把这个整数对应二进制的序列中的0变成-1,1还是1,得到一个1和-1组成的向量
- 把每个词哈希后的向量乘以词的权重,得到一个新的加权向量
- 把每个词的加权向量相加,得到一个最终向量,这个向量中每个元素有正有负
- 把最终这个向量元素为正的替换成1, 为负的替换成0,这个向量变成一个二进制位序列,也就是最终变成了一个整数
在Simhash过程中,可以发现权重小不太最要的词对最终的整数没有影响,这样那些不太重要的词就不影响内容之间的重复检测。
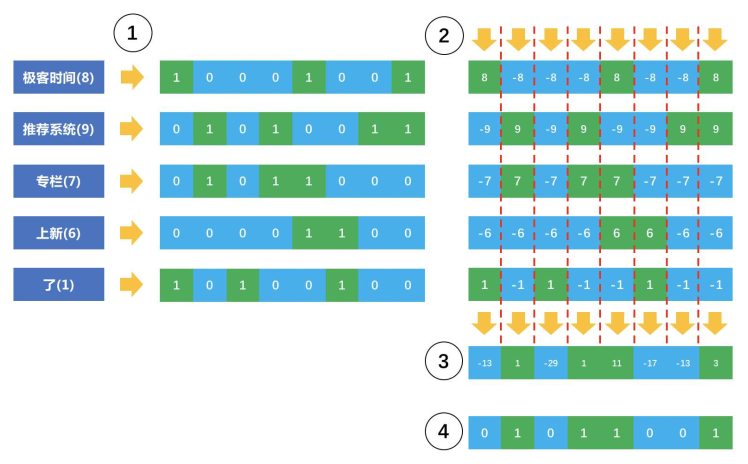
Simhash流程图
Simhash为每一个内容生成一个整数指纹,关键是把每个词哈希成一个整数,通常采用Jenkins算法。上图中只使用了8个二进制位,实际上可以需要64或者更多的二进制位表示。
得到每个内容的Simhash指纹后,可以两两计算汉明距离,比较二进制位不同的个数,实际上就是在计算两个指纹的异或,两个数越接近,异或结果0越多,1越少,如果异或结果包含3个以下的1,则认为两条内容重复。
推荐去重:布隆过滤器
推荐去重和内容源去重最大的不同就是过滤对象不同,上述Simhash过滤对象是内容本身,而推荐去重的对象是内容ID,即一般是一个用UUID表示的不太长的字符串或者整数。
对于这种模式串的去重,可以使用单独专门的数据库来保存,为了高效,甚至可以为它建立索引。但是用户量巨大的时候,做个方法对内存的消耗很高。
针对查看一个字符串在不在一个集合中的问题,有一个有点老但是很好用的方法,就是布隆过滤器Bloomfilter,它主要包含两个部分:
- 一个很长的二进制向量
- 一系列不同的哈希函数
布隆过滤器原理
- 设计n个互相独立的哈希函数,准备一个长度为m的二进制向量,最开始全是0
- 每个哈希函数把集合内的元素映射为一个不超过m的正整数k,m就是二进制向量的长度
- 把这个二进制向量中的第k个位置设置为1,也就是一个元素会在二进制向量中对应n个位置为1
- 在查询阶段,每个哈希函数将待查询的模式串s映射为n个整数,然后去查看二进制向量中n个整数对应的位置上是否为1,如果n个位置都为1,则可能已经存在s,但是如果没有1,则一定不存在该模式串s
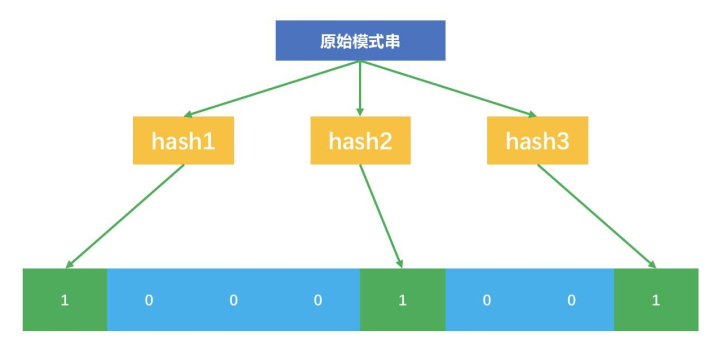
Bloomfilter流程图
布隆过滤器有小概率会把原本不属于集合中的模式串判断为存在,这样会导致那些明明没有被推荐的给用户的内容ID不被推荐给用户,当然,这是非常小概率事件,一般可以接受。
对于从布隆过滤器中的删除一个元素,业界一般不直接对布隆过滤器剔除元素,原因是剔除已有元素有可能导致整体数据错误。解决方法是使用Counting Bloom Filter支持删除操作,除了已有的二进制向量,向量的每一位对应一个整数计数器,每当增加一个元素时,哈希函数映射到的二进制向量位的整数计数器加1,删除时减1,有了这个操作可以增加,查找和删除集合里的元素。 缺点是这样会消耗大量内存。

其他算法思维导图
本文是《推荐系统三十六式》的读书笔记,仅限个人学习,请勿用作商业用途,谢谢。
Note: Cover Picture
