算法与数据结构入门篇
基础知识就像是一座大楼的地基,它决定了我们的技术高度,而要想快速做点事情,前提条件一定是基础能力过硬,”内功“要到位。
从广义上讲,数据结构就是一组数据的存储结构,算法就是操作数据的一组方法。
数据结构是为算法服务的,算法要作用在特定的数据结构之上。
数据结构和算法解决的是如果更快、更省地存储和处理数据的问题,因此,我们就需要一个考量效率和资源消耗的方法,这就是复杂度分析方法。
专栏重点
本专栏中,重点学习20个最常用的数据结构和算法:
10个数据结构
- 数组
- 链表
- 栈
- 队列
- 散列表
- 二叉树
- 堆
- 跳表
- 图
- Trie树
10个算法
- 递归
- 排序
- 二分查找
- 搜索
- 哈希算法
- 贪心算法
- 分治算法
- 回溯算法
- 动态规划
- 字符串匹配算法
复杂度分析:如何分析、统计算法的执行效率和资源消耗
将代码跑一遍,通过统计、监控,就能得到算法执行的时间和占用的内存大小,这种估计算法复杂度的方法叫做事后统计法,但是,有非常大的局限性:
- 测试结果非常依赖测试环境:测试环境中硬件的不同会对测试结果有很大的影响
- 测试结果受数据规模的影响很大
我们需要一个不用具体的测试数据来测试,就可以粗略估计算法的执行效率的方法。
大O复杂度表示法
T(n)代表代码执行的时间;n表示数据规模的大小;f(n)表示每行代码执行的次数总和;公式中的O表示代码的执行时间T(n)与f(n)表达式成正比。
大O时间复杂度并不具体代表代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫做渐进时间复杂度(Asymptotic time complexity),简称时间复杂度。
当n非常大时,公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略,只需要记录最大量级的代码就可以了。
时间复杂度分析
- 只关注循环执行次数最大的一段代码:这段核心代码执行次数的n的量级,就是整段要分析代码的时间复杂度
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
- 乘法法则:嵌套代码的复杂度等于嵌套内外复杂度的乘积
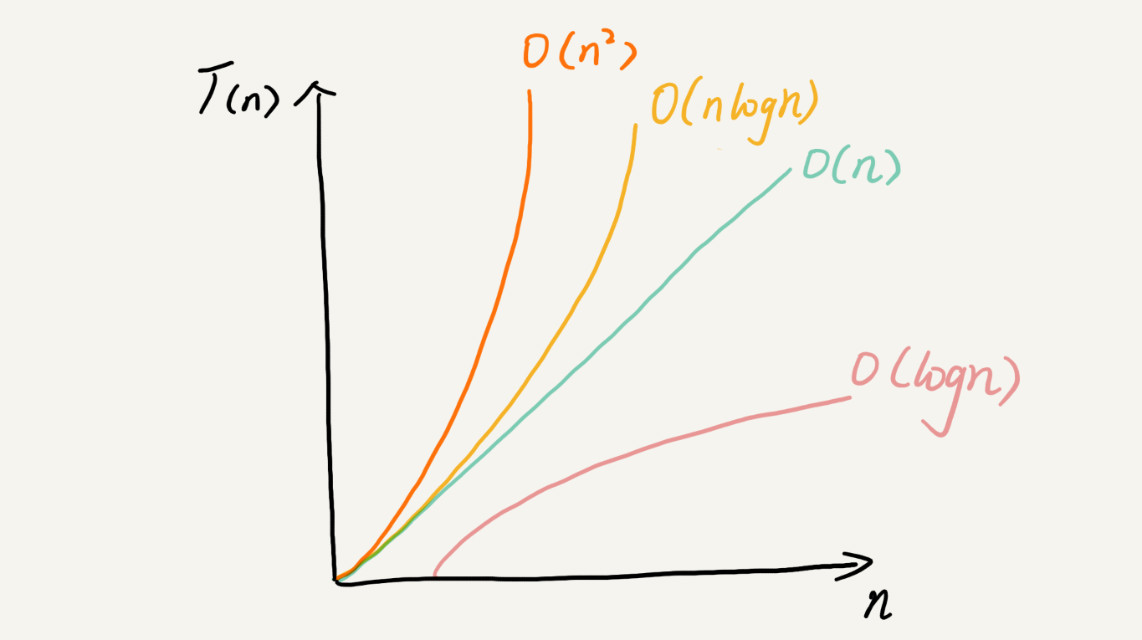
常见复杂度量级
常见的时间复杂度量级如下:

可以将其粗略地分为多项式量级和非多项式量级,后者只有两个:O(2^n)和O(n!). 当数据规模n越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增长,是非常低效的算法。
O(1)
O(1)只是常量级时间复杂度的一种表示方法,并不代表代码只执行了一次。
一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行代码,其时间复杂度也是O(1).
O(logn)、O(nlogn)
不管以多少为底,统一将对数阶的时间复杂度都记为O(logn)。因为可以转换对数:
其中log_{m}{l} 是一个常数,可以省略。
归并排序、快速排序的时间复杂度都是O(nlogn).
O(m+n)、O(m*n)
代码的复杂度由两个数据的规模来决定。
空间复杂度分析
空间复杂度的全称是渐进空间复杂度(Asymptotic space complexity),表示算法的存储空间与数据之间的增长关系。
常见的空间复杂度是O(1)、O(n)、O(n^2).
复杂度分析关键在于多练,所谓熟能生巧。
复杂度分析:浅析最好、最坏、平均、均摊时间复杂度
同一段代码在不同情况下时间复杂度会出现量级差异,为了更全面,更准确的描述代码的时间复杂度,引入了最好、最坏、平均和均摊时间复杂度的概念。代码复杂度在不同情况下出现量级差别时才需要去区别则四种复杂度。大多数情况下,是不需要区别分析它们的。
最好、最坏时间复杂度
- 最好时间复杂度是在最理想的情况下,执行这段代码的时间复杂度。
- 最坏时间复杂度是在最糟糕的情况下,执行这段代码的时间复杂度。
平均时间复杂度
平均情况下的随时间复杂度简称为平均时间复杂度,严格意义上来说应该是加权平均时间复杂度或者期望时间复杂度。
均摊时间复杂度
通过摊还分析得到的时间复杂度叫做均摊时间复杂度。在代码执行的所有复杂度情况中绝大部分是低级别的复杂度,个别情况是高级别复杂度且发生具有时序关系时,可以将个别高级别复杂度均摊到低级别复杂度上,基本上均摊结果就等于低级别复杂度。
平均和均摊基本上就是一个概念,均摊是特殊的平均,当出现O(1)的次数远大于出现O(n)的次数的时候,平均平摊时间复杂度就是O(1).
注:本文是《数据结构与算法之美》的读书笔记,配套代码地址GitHub。本文仅限个人学习,请勿用作商业用途,谢谢。
Note: Cover Picture
