数据结构与算法-查找

二分查找

二分查找针对的是一个有序的数据集合，思想是折半查找，类似分治思想，每次都通过更区间的中间元素对比，将待查找的区间缩小为原来的一半，直到找到要查找的元素，或者区间被缩小为0，时间复杂度是O(logn)。

下图是猜一个数的过程：

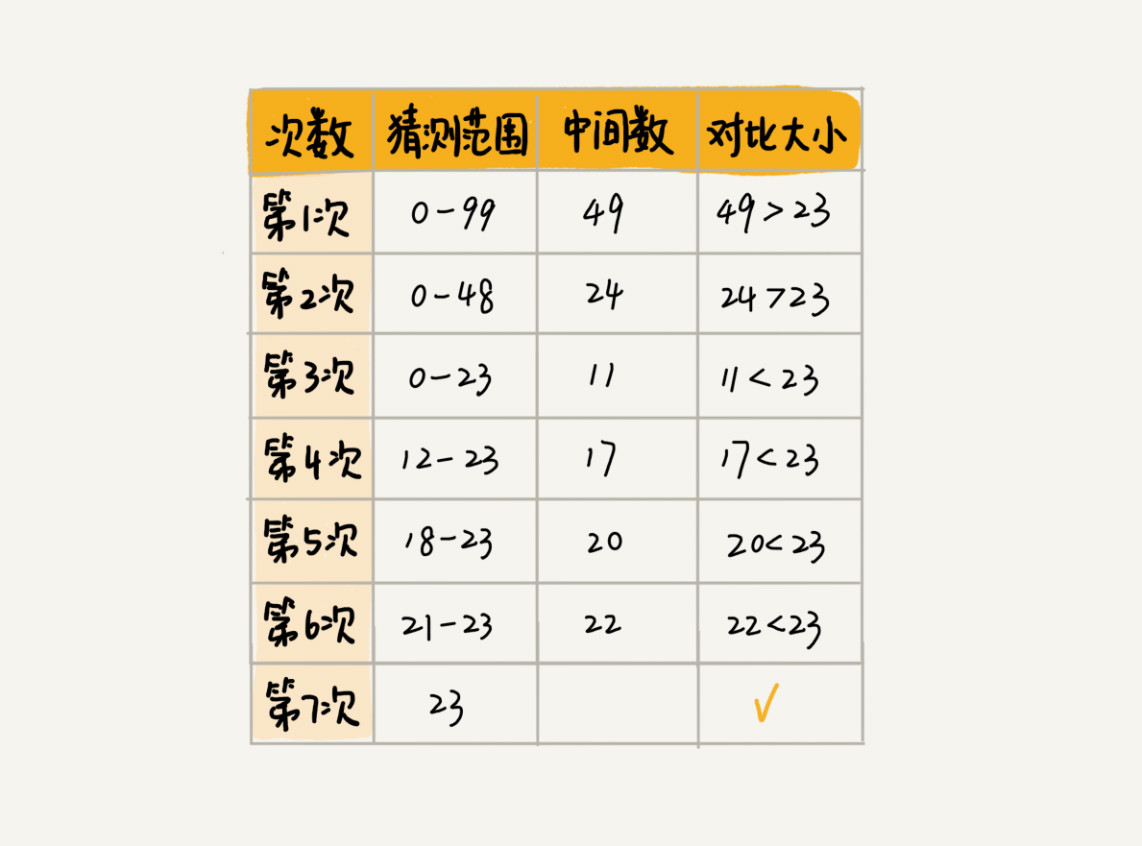
下图代表二分查找的过程：

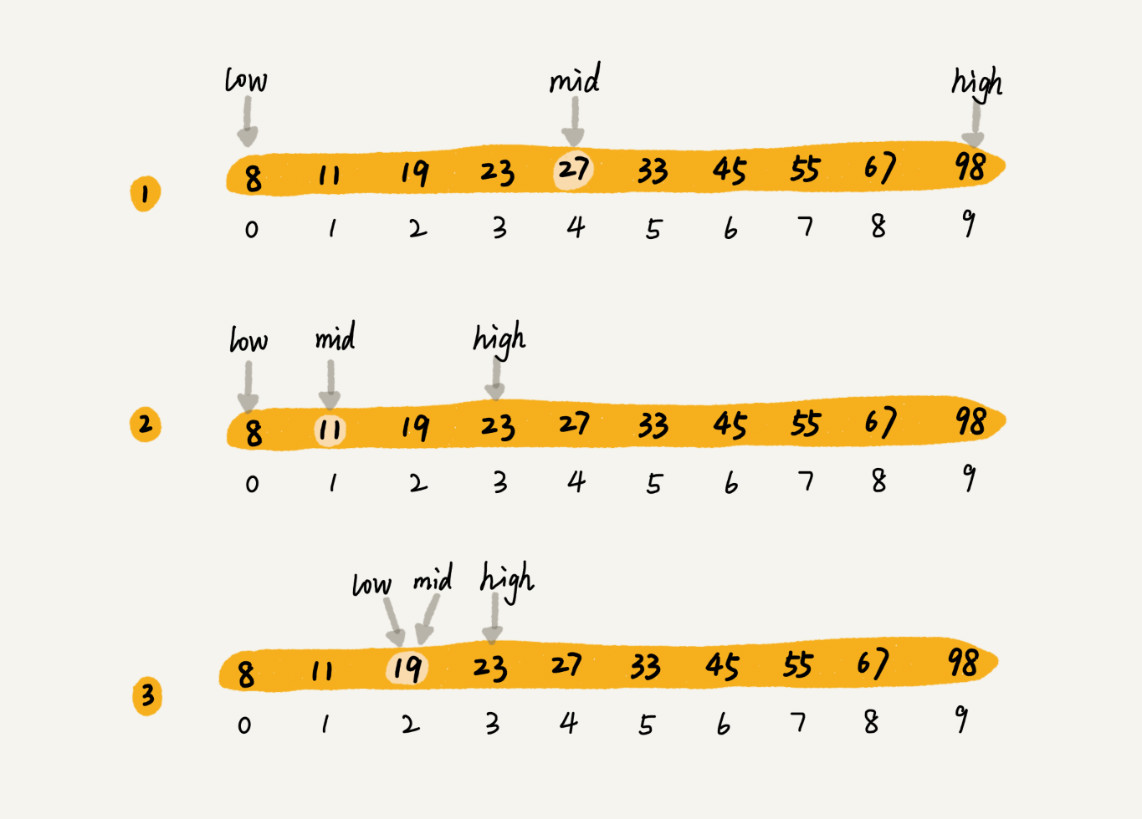
常量级时间复杂度的算法有可能还没有O(logn)的算法执行效率高。

二分查找的递归和非递归实现

针对最简单的不存在重复元素的有序数组，Java版本的二分查找的递归实现是：

public int binary_search(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  
  // 注意循环条件
  while (low <= high) {

    // 注意溢出
    int mid = (low + high) / 2;
    if (a[mid] == value) {
      return mid;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }

  return -1;
}

容易出错的三个地方：

循环退出条件：是low <= high，而不是low < high
mid的取值：注意溢出，改进：
1. low + (high - low)/2
2. log + ((high - low) >> 1)：对于计算机来说，位运算的处理过程比除法快
low和high的更新：如果直接写成low=mid或者high=mid，会发生死循环
1. low = mid + 1
2. high = mid - 1

二分查找的递归实现：

// 二分查找的递归实现
public int binary_search(int[] a, int n, int val) {
  return binary_search_internally(a, 0, n - 1, val);
}

private int binary_search_internally(int[] a, int low, int high, int value) {
  if (low > high) return -1;

  int mid =  low + ((high - low) >> 1);
  if (a[mid] == value) {
    return mid;
  } else if (a[mid] < value) {
    return binary_search_internally(a, mid+1, high, value);
  } else {
    return binary_search_internally(a, low, mid-1, value);
  }
}

二分查找应用场景的局限性

二分查找的应用场景有很大的局限性，只能用在插入、删除操作不频繁，一次排序多次查找的场景中：

二分查找依赖的是顺序表结构：简单点说就是数组，不能用链表，因为二分查找算法需要按照下标随机访问元素，链表不支持随机访问。二分查找只能用在数据是通过顺序表来存储的数据结构上
二分查找针对的是有序数据：对于静态数据，一次排序，多次二分查找效率高；对于动态数据，查找之前需要排序，效率低
数据量太小不适合二分查找
数据量太大也不适合二分查找：因为需要用连续的内存空间存储数据如数组，如果数据量太大，没有连续的内存存储数据也不行

如何用最省内存的方式实现快速查找功能

如何在1000万个整数中快速查找某个整数？内存限制是100MB，每个数据大小是8字节。

最简单的方法就是将数据存储在数组中，内存占用差不多是80MB，符合内存限制。然后对这1000万个整数进行排序，再利用二分查找算法，就可以快速地查找想要的数据了。

但是这题不能用散列表、二叉树做，因为除了原始的整数数据之外，散列表和二叉树都需要额外的内存空间，100MB内存就不够了。二分查找不需要额外的存储空间，是最节省空间的存储方式，能在限定内存大小的前提下解决这个问题。

二分查找的变形问题

查找第一个值等于给定值的元素
查找最后一个值等于给定值的元素
查找第一个大于等于给定值的元素
查找最后一个小于等于给定值的元素

查找第一个值等于给定值的元素

代码1如下：

public int binary_search(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid = low + ((high - low) >> 1);
    if (a[mid] >= value) {
      high = mid - 1;
    } else {
      low = mid + 1;
    }
  }

  if (low < n && a[low]==value) return low;
  else return -1;
}

代码2如下：

public int binary_search(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
        // 如果mid等于0，即数组第一个元素，代表肯定是我们要找的下标，如果mid不等于0，但是a[mid]的前一个元素a[mid-1]不等于value，说明此时的a[mid]就是我们要找的值
      if ((mid == 0) || (a[mid - 1] != value)) return mid;
      // 如果a[mid]==value,但是并不是第一个重复的元素，就将high赋值为mid-1，往前走一步之后继续判断，因为要找的元素一定出现在[low, high-1]之间
      else high = mid - 1;
    }
  }
  return -1;
}

查找最后一个值等于给定值的元素

代码如下，思路和上一个类似：

public int binary_search(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

查找第一个大于等于给定值的元素

public int binary_search(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] >= value) {
      if ((mid == 0) || (a[mid - 1] < value)) return mid;
      else high = mid - 1;
    } else {
      low = mid + 1;
    }
  }
  return -1;
}

查找最后一个小于等于给定值的元素

public int binary_search7(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

如何快速定位IP对应的省份地址

当我们查找某个IP归属地时，先通过二分查找，找到最后一个起始IP小于等于这个IP的IP区间，然后检查这个IP是否在这个IP区间内，如果在，我们就取出对应的归属地显示，如果不在，就返回未查找到。

注：本文是《数据结构与算法之美》的读书笔记，配套代码地址GitHub。本文仅限个人学习，请勿用作商业用途，谢谢。

Note: Cover Picture

Super Agents of AI