Collaborative Filtering
Average Rating
Basic algorithms is to make s(j) the average rating for j:
$$ s(i,j) = \frac{\sum_{ {i} \in \omega_j} r_{ij}}{| \omega_j |} $$
- s(i,j) can depend both on user i and item j
- Omega_j = Set of all users who rated item j
- r_ij = rating user i gave item j
- i: [1,N], N is the number of users
- j: [1,M], M is the number of items
Some Issues of Average Rating
It treats everyone’s rating of the movie equally.
Sparsity
R_{N*M} = user - items ratings matrix of size N * M, User-item matrix is sparse because most entries are empty!
Goal of Collaborative Filtering
- We want to make recommendations
- Most of r(i,j) doesn’t exist, this is good
- Dense matrix is convenient mathematically, but sucks business-wise
- It means every user has already seen every movie, so we have nothing to recommend
- Therefore, the matrix must be sparse in order to actually have items to recommend
Regression
Since we want to predict a real number, so objective is MSE:
$$ MSE = \frac{1}{\omega} \sum_{i,j \in \omega}(r_{ij} - \bar{r}_{ij})^2 $$
omega is the set of pairs (i,j) where user i has rated item j.
User-User Collaborative Filtering
For UCF, the goal is to find the “users like me”. It’s intuitive that if they are “like me”, I’d like movies they’ve rated highly.
The user-item matrix is shown below:
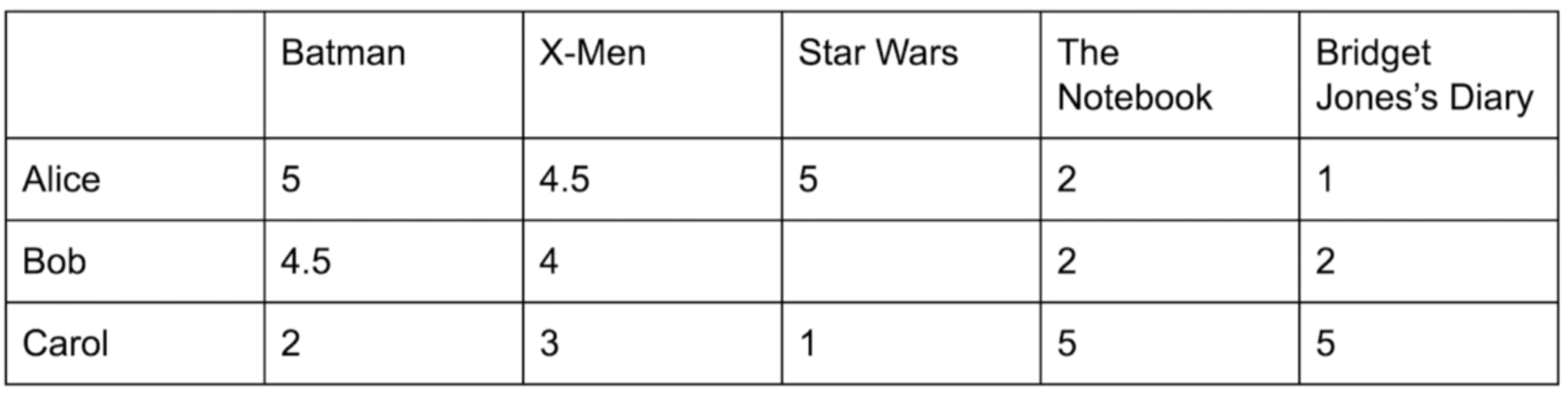
We can see that Alice’s and Bob’s ratings are highly correlated.
Weighted Ratings
Intuitively, I want it to be small for users I don’t agree with, large for users I do agree with:
$$ s(i,j) = \frac{\sum_{ {i,i\prime} \in \omega_j} W_{ii\prime} r_{ij}}{ \sum_{i,i\prime \in \omega_j} W_{ii\prime}} $$
W_ii’ is the weight between user i and user i’.
Deviation
We care how much it deviates user’s own average, but not the absolute rating:
$$ dev(i,j) = r(i,j) - \bar{r_i}, for \ a \ known \ rating $$
The deviation score for use i gave item j is the rating user i gave j minus the average rating of user i across all movies.

Deviation + Weighted Ratings
The score function combining deviation and weighted ratings is shown below:
$$ s(i,j) = \bar{r_i} + \frac{\sum_{ {i,i\prime} \in \omega_j} W_{ii\prime} | r_{i\prime j} - \bar{r}_{i\prime} | }{ \sum_{i,i\prime \in \omega_j} W_{ii\prime}} $$
How to Calculate Weights
Pearson Correlation Coefficient
$$ P(x,y) = \frac{\sum_{i=1}^{N} (x_i - \bar{x}) (y_i - \bar{y})}{\sqrt{\sum_{i=1}^{N} (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^{N} (y_i - \bar{y})^2}} $$
The problem is our matrix is sparse. So we could modify the formula to this:

Cosine Similarity
$$ \cos \theta = \frac{x^T y}{ |x| |y| } = \frac{\sum_{i=1}^{N} x_i y_i}{ \sqrt{\sum_{i=1}^{N} x_i ^2} \sqrt{\sum_{i=1}^{N}y_i^2}} $$
Cosine Similarity VS Pearson Correlation Coefficient
They are the same! Except Pearson is centered. We want to center them anyway because we’re working with deviations, not absolute ratings.
Problem
- If 2 users have zero movies in common, don’t consider i’ in user i’s calculation-it can’t be calculated
- If few(e.g. < 5) then don’t use the weight, since not enough data to be accurate
Neighborhood
- In practice, don’t sum over all users who rated movie j (takes too long)
- It can help to pre-compute weights beforehand
- Non-trivial: instead of summing over all users, take the ones with the highest weight. E.g. use K nearest neighbors, K = 25 up to 50
Item-Item Collaborative Filtering
The correlation between the column vectors is high. If you like Power Rangers, you’ll also like Transformers.
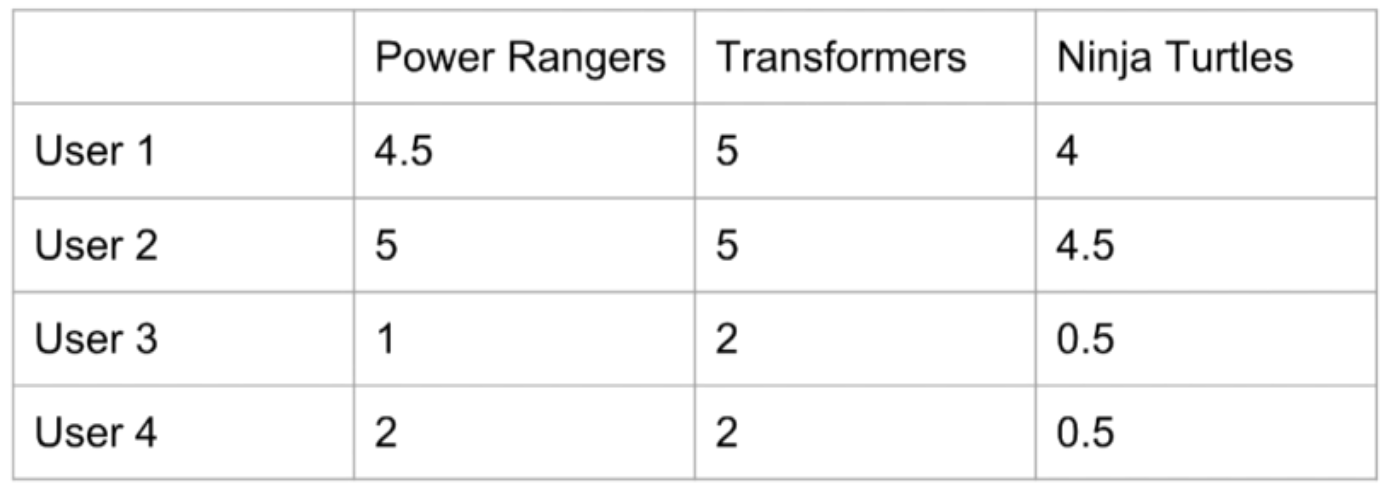
Hot to Calculate Weights for Item Correlation

Item Score
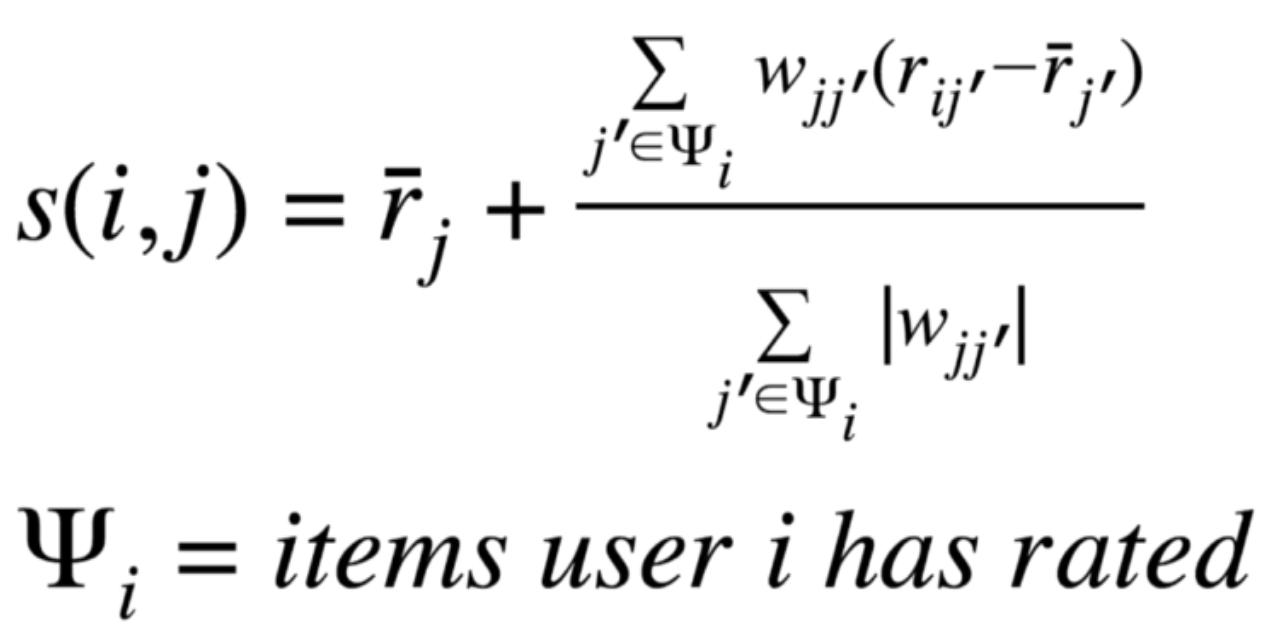
The deviation means how much user i likes item j’, compared to how much everyone else like j’. If user i really like j’(more than other users do) and j is similar to j’(w_jj’ is high), then user i probably likes j too.
UCF VS ICF
- UCF: Choose items for a uses, because those items have been liked by similar users
- ICF: Choose items for a user, because this user has liked similar items in the past
UCF and ICF are mathematically identical.

Summary
For average rating which considers only a single score for each item regardless of which user is looking. Some problems:
- Not all rating should be treated equally
- Users who I agree with should be weighted higher
- Users I disagree with should be weighted lower
By using collaborative filtering method, the s(i,j) score depends on user i and item j. We used the pearson correlation as weights.
By flipping the rating matrix sideways, we can convert our UCF algorithm into an ICF algorithm.
But accuracy is not the most important thing we care about since it can leads to lack of diversity in recommendations which always suggesting “similar products”.
The user-item matrix doesn’t have to be ratings at all!
Note: Cover Picture
