Simple Recommender System
Popularity
Simple algorithm to sort by popularity:
select article_id from articles order by page_views desc;
“Other people really like this, therefore, you’ll probably like it too.”
Product Association
Using Life to measure the association between products:
$$ Lift = \frac{P(A,B)}{P(A)P(B)} = \frac{P(A | B)}{P(A)} = \frac{P(B | A)}{P(B)} $$
- Symmetric
- If A&B are independent, then P(A|B) = P(A), so Lift=1
- If buying increases the probability you buy A, the Lift > 1
Hacker News
Balancing popularity with age:
$$ \frac{f(popularity)}{g(age)} $$
Hacker News Formula:
$$ score = \frac{(ups - downs - 1)^{0.8}}{(age + 2)^{gravity}} \times penalty $$
- gravity = 1.8 > 0.8
- penalty = multiplier to implement “business rules”
- Denominator grows faster than numerator,age always overtakes popularity
Link popularity has been found to follow power law/logn tail. Scores decrease over time.
Reddit Formula:
$$ score = sign(ups - downs) \times \log{\max{(1, | ups - downs |)}} + \frac{age}{45000} $$
- Always positive
- Newer links -> more score
- scores will forever increase linearly
Rating
At a high level, you can think of:
- binary outcomes as classification
- 5 star ratings as regression
The average rating can’t show the real popularity between products.
Confidence Intervals
- Given a random variable X, we can calculate the distribution of its sample mean
- The more samples I collect (N), the skinnier its distribution:
$$ \bar{X} = \frac{1}{N} \sum_{i=1}^{N} X_i, X \sim N(\mu, \sigma^2), \bar{X} \sim N(\mu, \frac{\sigma^2}{N}) $$
Explore-Exploit Dilemma
Bayesian approach to the EE problem:
- Min theme: “Everything is a random variable.”
- Random variable have a probability distribution, parameters,…
$$ P(\pi | X) = \frac{P(X|X)P(\pi)}{\int_{0}^{1} P(X|X)P(\pi) d\pi } $$
In general, posterior = likelihood * prior / normalizing constant
Key is to rank by samples drawn from posteriors, since each item has its own posterior.
Automatically balances between explore and exploit.
Sampling the posterior is “intelligently” random rather than totally random since it accounts for the data we’ve collected.
Bayesian Bandit: Code
Supervised Learning
- We have some inputs(X) and corresponding targets(Y)
- Y might represent:
- Did the user by the product?
- Click on the ad?
- Make an account?
- If our model predicts are accurate, then we can use it to recommend items the user is more likely to buy / click / rate highly.
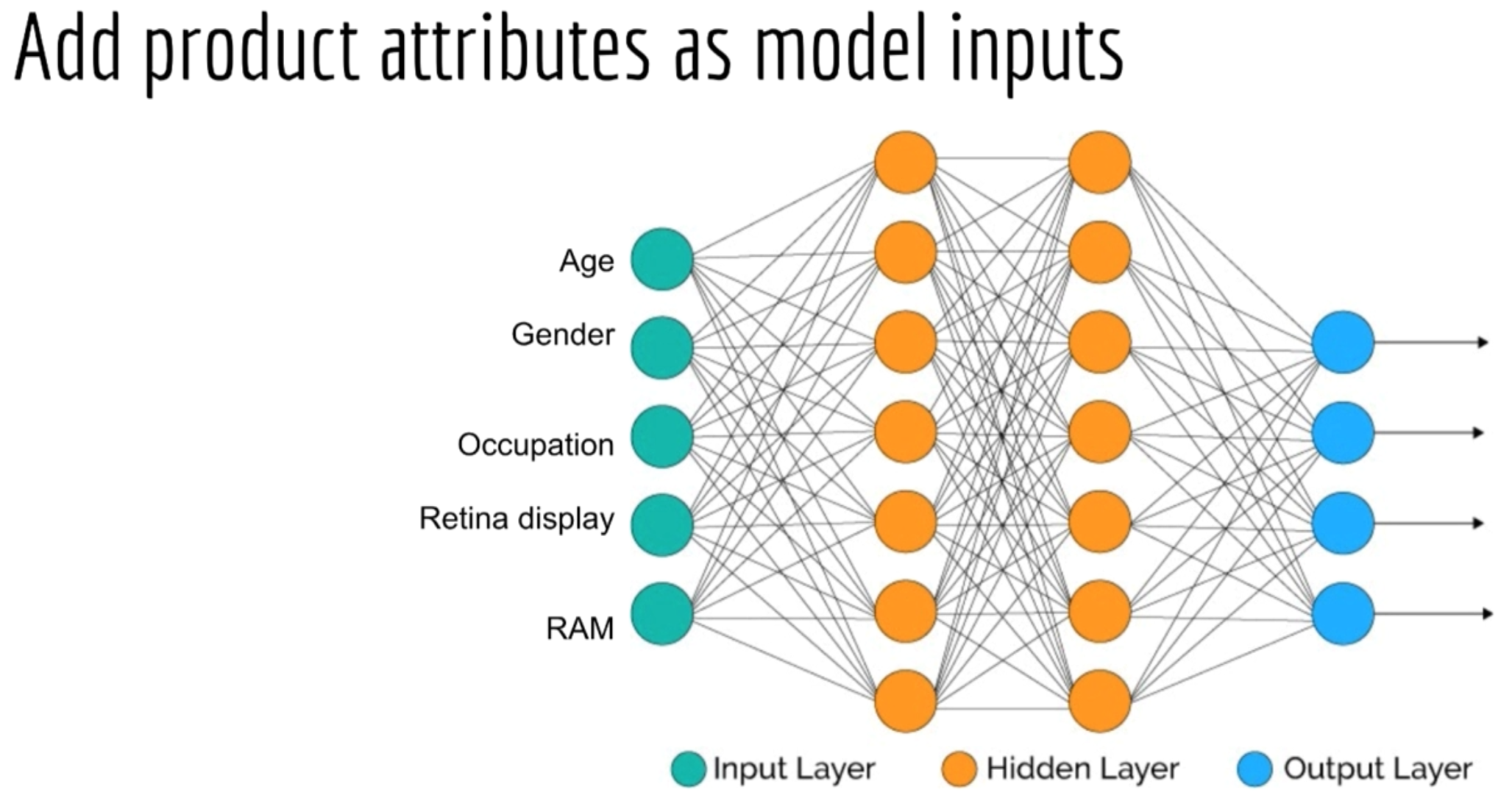
Input Features
- Common features include demographics:
- Age
- Gender
- Religion
- Location
- etc.
- i.e. data the government collects
- Any other data collected by your site
- Can purchase data from other companies
Building a model
Instead of building a separate model for each produce, we can combine the user and product attributes as input features of a neural network model.
Note: Cover Picture
