Super Agents of AI

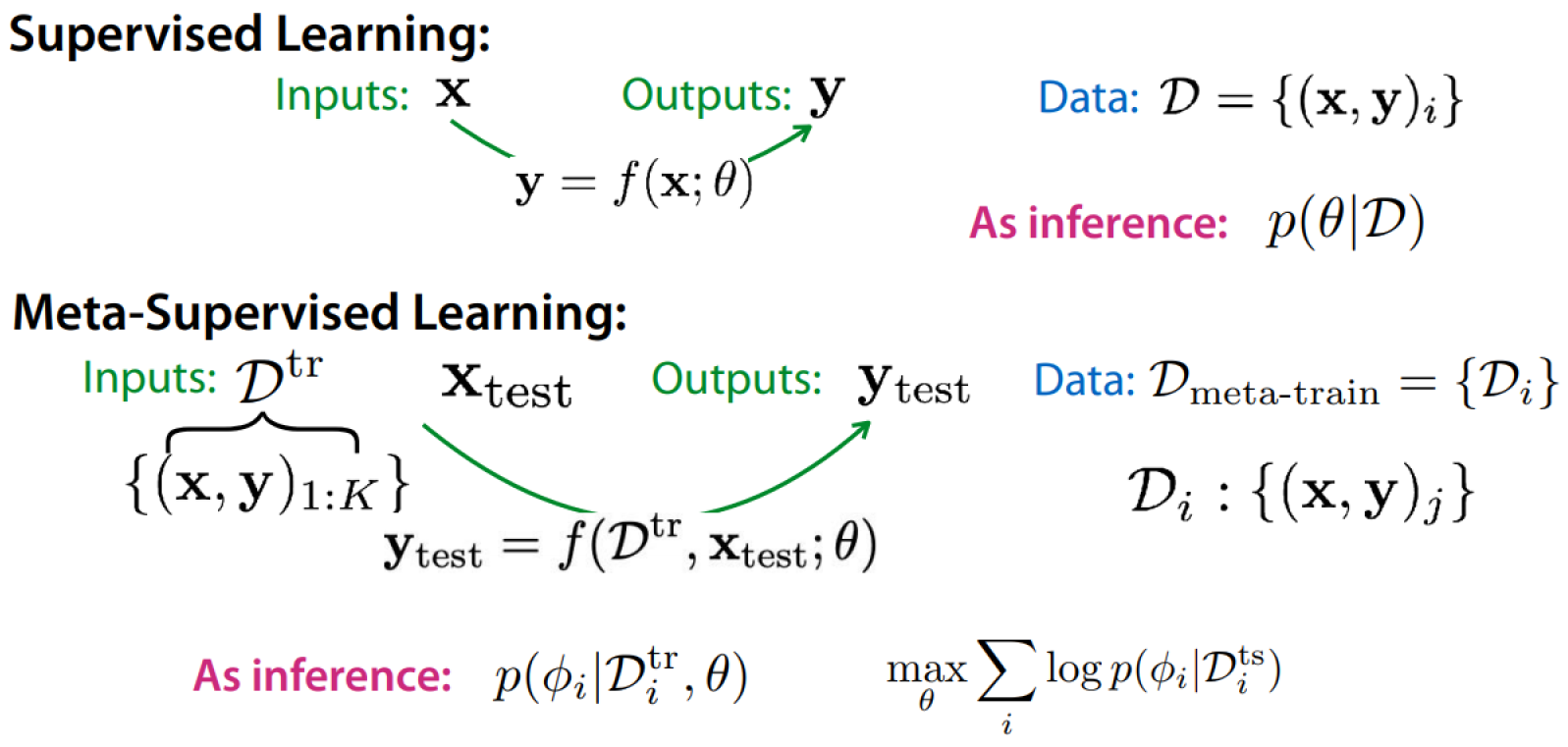
Meta-Learning

Definition of meta-learning:

The probabilistic view of meta-learning:

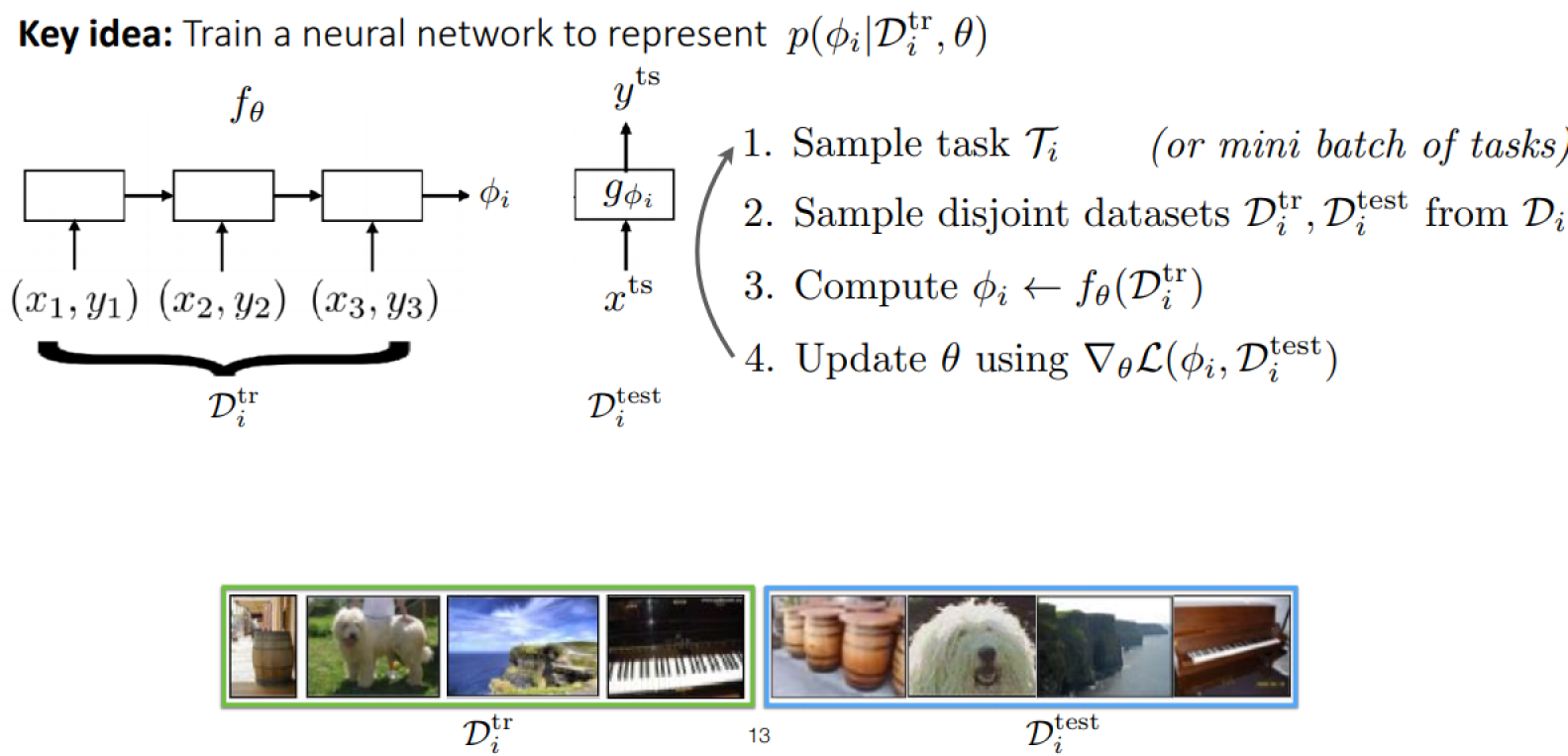
How to design a meta-learning algorithm

1. Choose a form of $p(\phi_i | D_i^{tr}, \theta)$
2. Choose how to optimize $\theta$ w.r.t max-likelihood objective using $D_{meta-train}$

Black-Box Adaptation

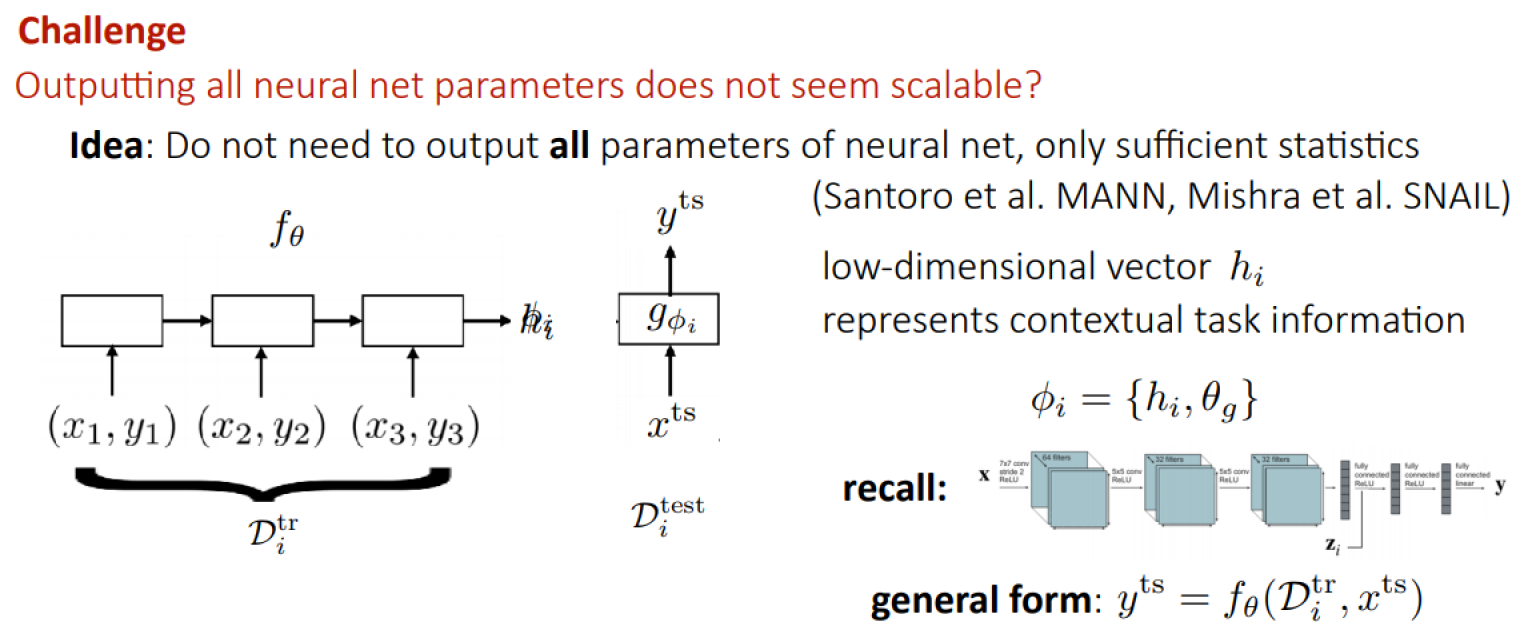
Challenge

Pro:

1. Expressive
2. Easy to combine with variety of learning problems(e.g. SLk, RL)

Con:

1. Complex model w/ complex task: challenging optimization problem
2. Often data-inefficient

Optimization-Based Inference

Fine-tuning

Key idea: Acquire $\phi_i$ through optimization.

$\max_{\phi} \log p(D_i^{tr} | \phi_{i}) + \log p(\phi_{i} | \theta)$

This assumes meta-parameters $\theta$ serve as a prior. One successful form of prior knowledge is: Initialization for fine-tuning.

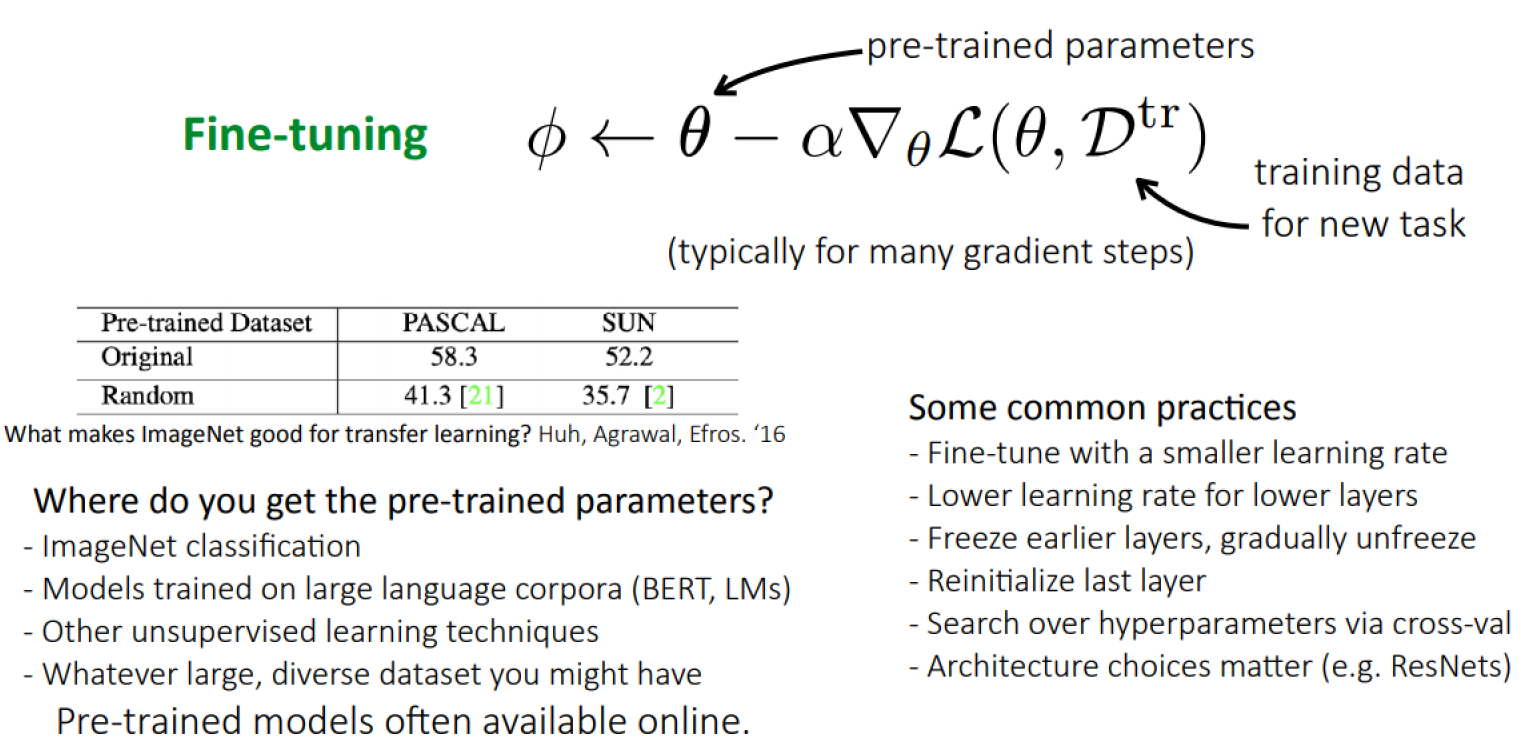
Fine-tuning is less effective with very small datasets.

Meta-learning

Key idea: Over many tasks, learn parameter vector $\theta$ that transfers via fine-tuning.

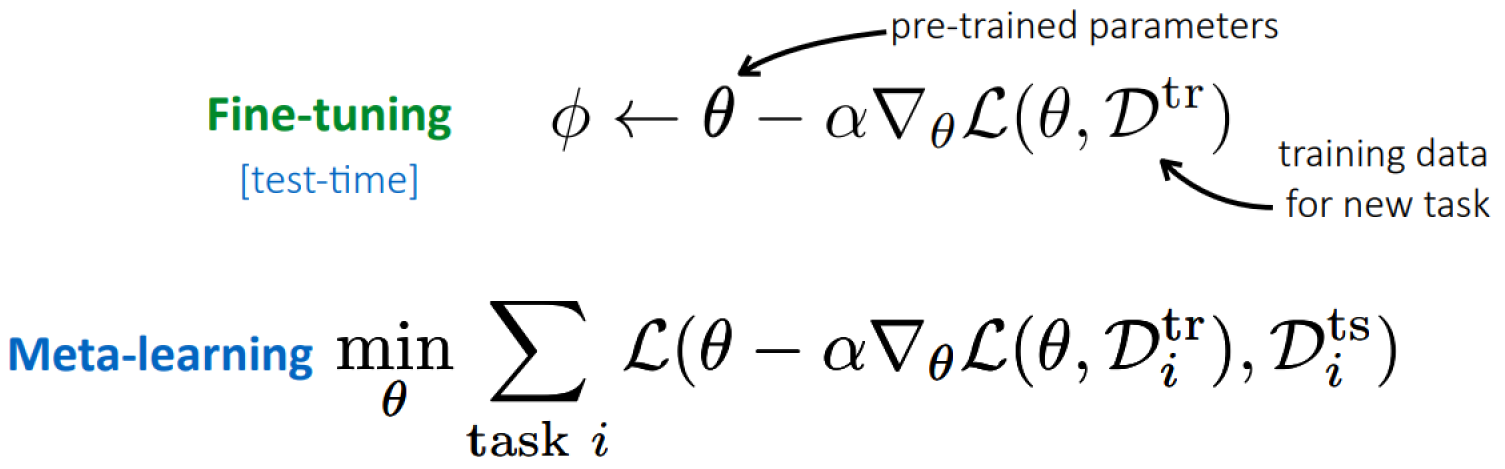
Model-Agnostic Meta-Learning

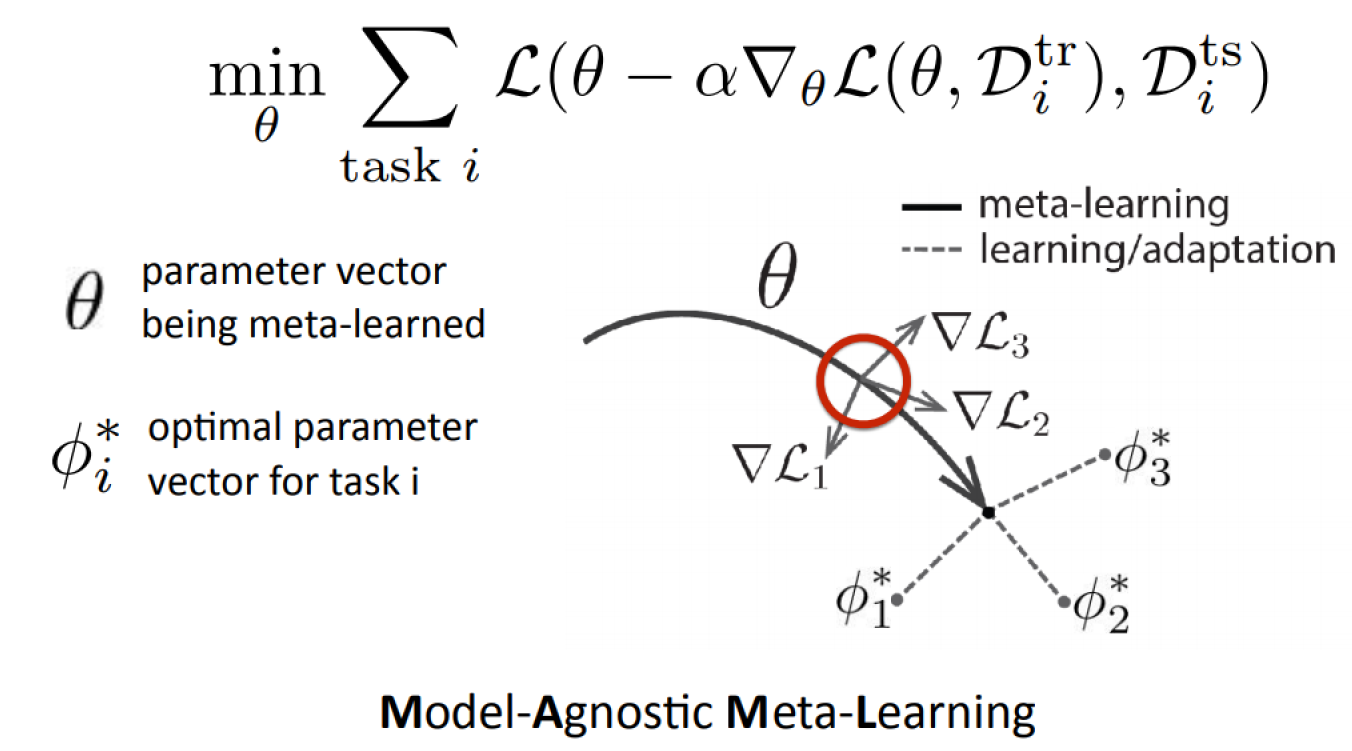
From: Finn, Abbeel, Levine. Model-Agnostic Meta-Learning. ICML 2017

Optimization vs. Black-Box Adaptation

For a sufficiently deep f, MAML function can approximate any function of $D_i^{tr}, x^{ts}$.

Challenge

How to choose architecture that is effective for inner gradient-step?

Idea: Progressive neural architecture search + MAML (Kim et al. Auto-Meta):

• Finds highly non-standard architecture (deep & narrow)
• Different from architectures that work well for standard supervised learning

Bi-level optimization can exhibit instabilities.

Back-propagating through many inner gradient steps is compute & memory intensive.

Idea: Derive meta-gradient using the implicit function theorem. Form Rajeswaran, Finn, Kakade, Levine. Implicit MAML, 2019

Note: Cover Picture