Policy Gradients
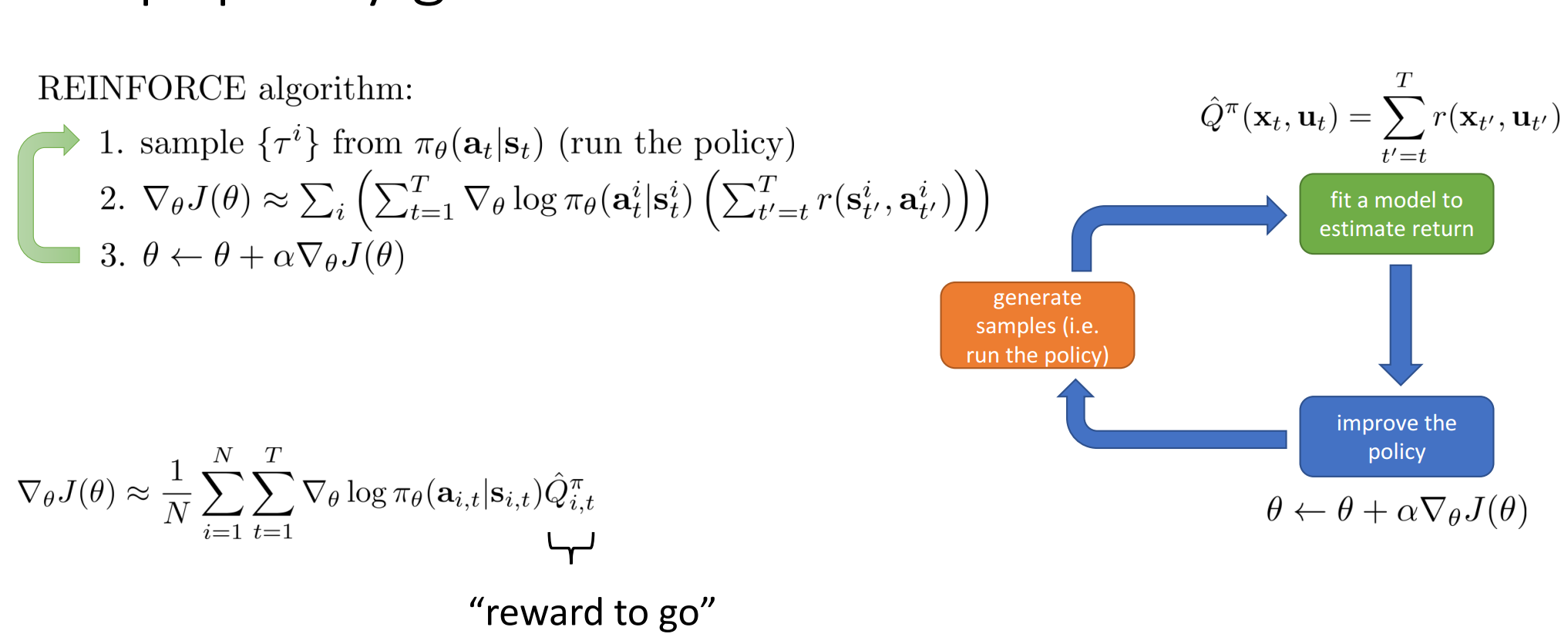
在策略梯度中的核心点就是在对”reward to go”即进行准确的估计。
Improving the Policy Gradient
简单的策略梯度方法仅仅使用一次轨迹样本,存在方差,因此改进版本利用多次样本的平均值作为期望reward来作为的更好的估计。

Add Baseline
为了减少策略梯度带来的方差,引入了baseline,可以是平均的reward,更好的选择是.
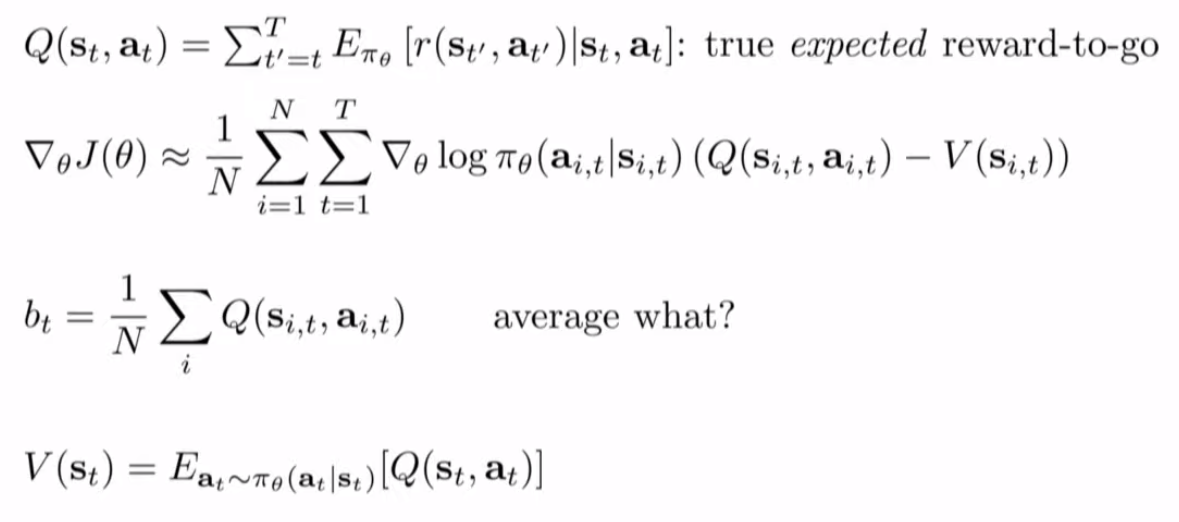
通常我们将Q值和V值的差定义为Advantage值,代表在t时刻的状态下执行动作有多好,即:
State & state-action value functions
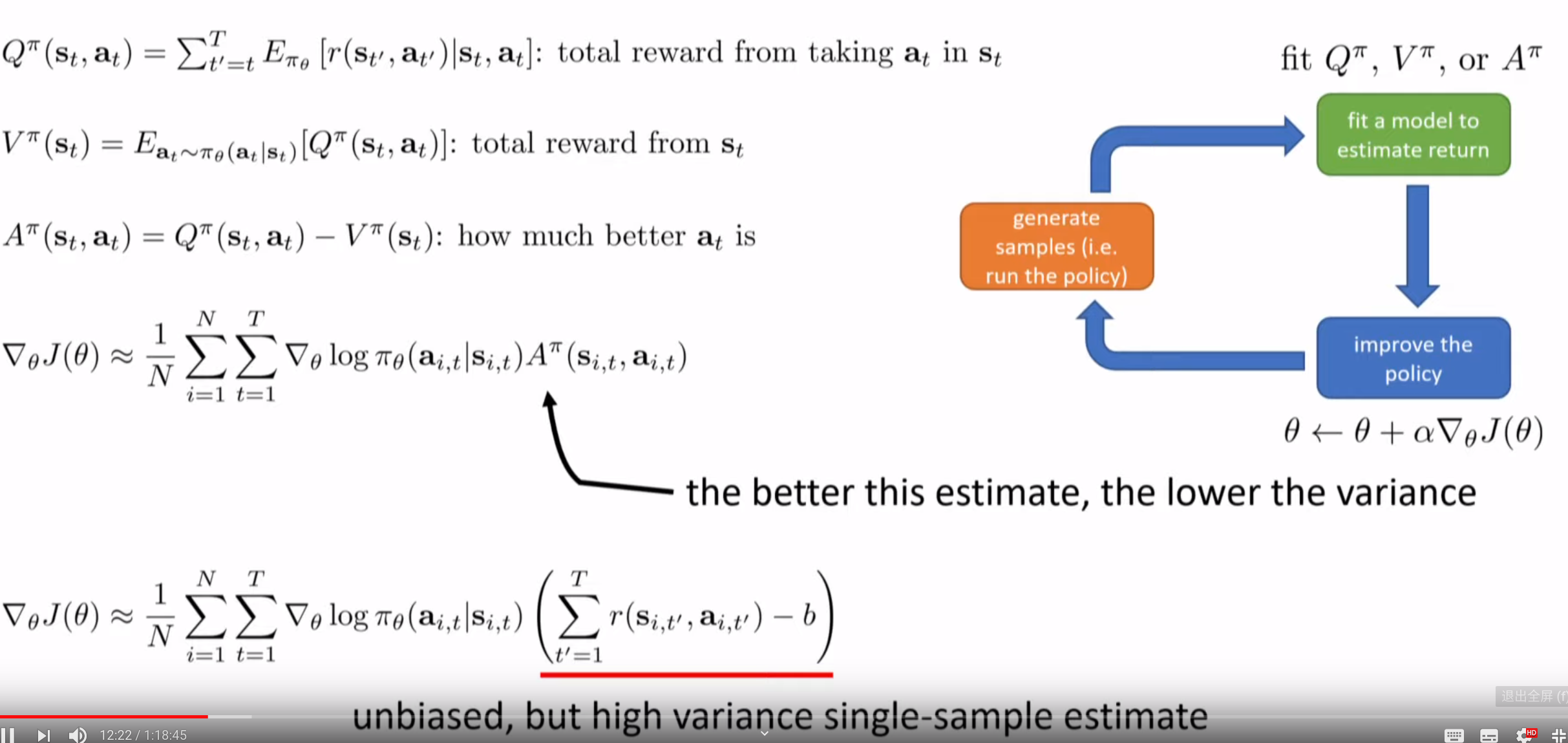
简单的添加baseline的策略梯度方法是无偏的但是高方差的单样本估计。
Value Function Fitting
在对Advantage值进行估计时,可以通过估计Q值或者V值来对A值进行估计,即:
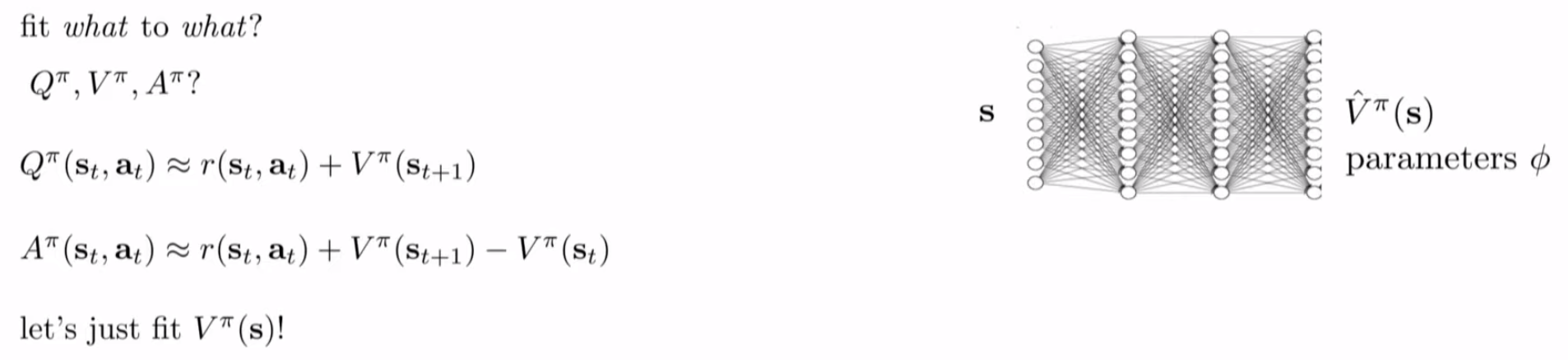
Policy Evaluation
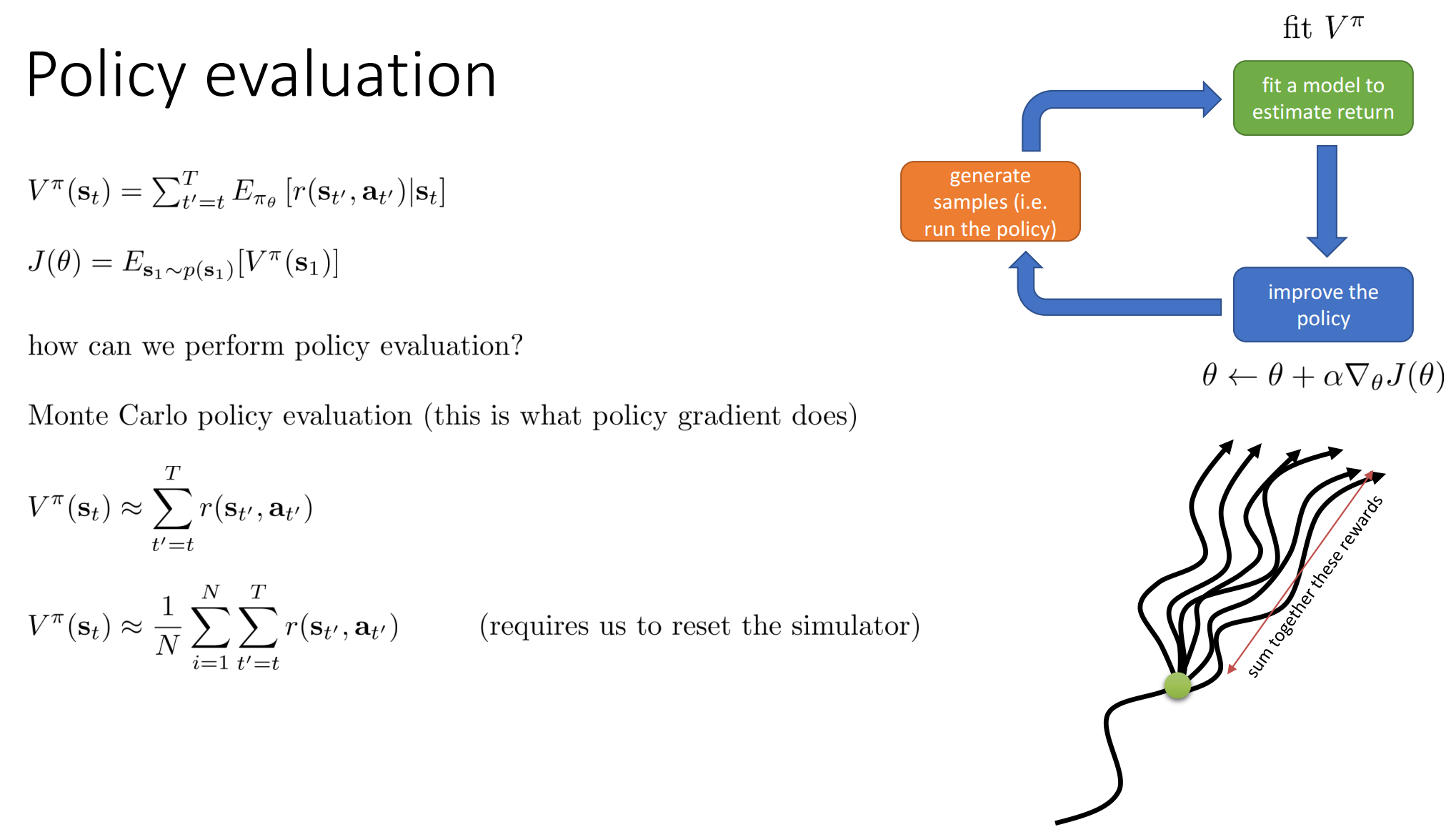
Monte Carlo Evaluation with Function Approximation
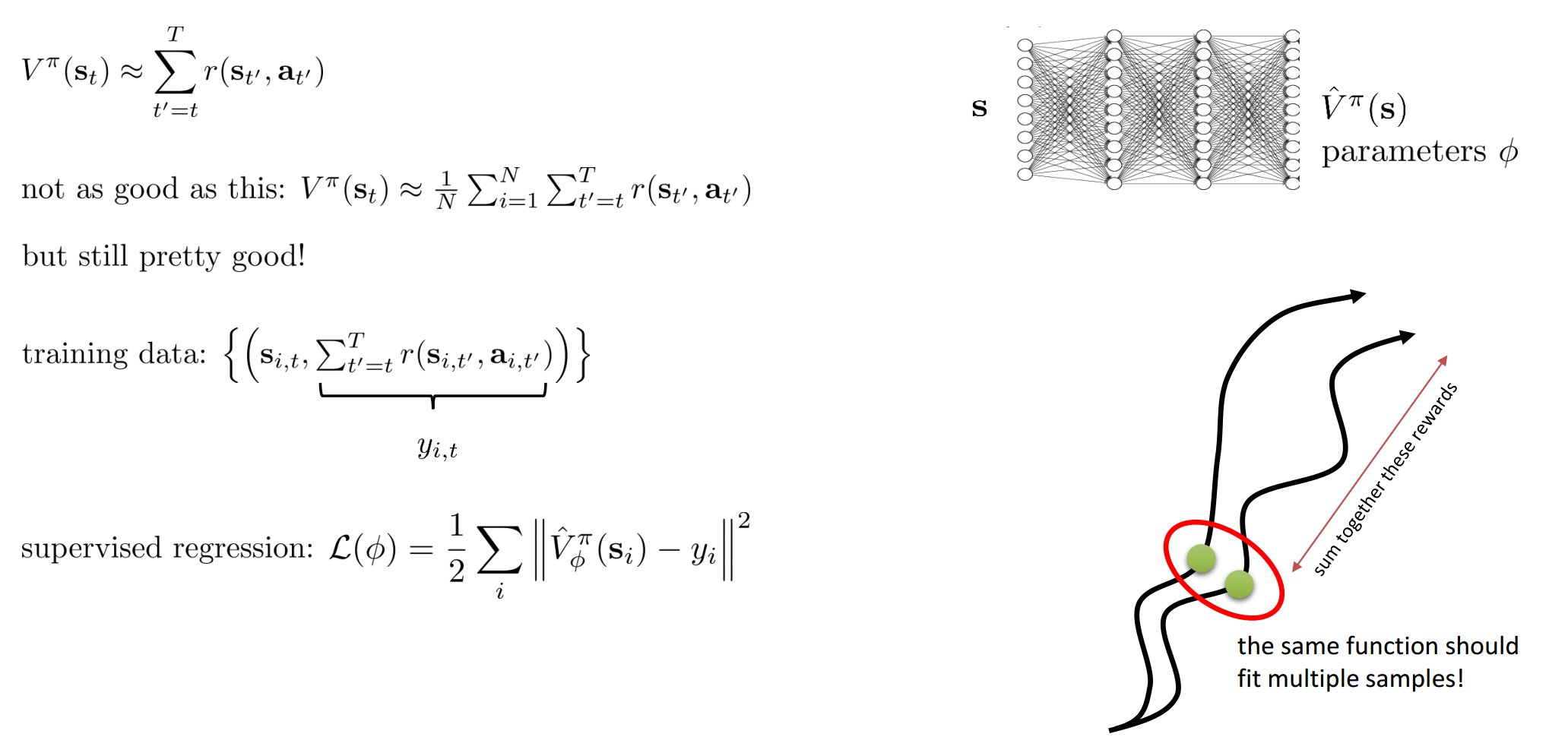
Improved Evaluation
蒙特卡洛是将整个轨迹的reward相加起来作为V值,但是该值并不是ideal的,因此改进版本为:

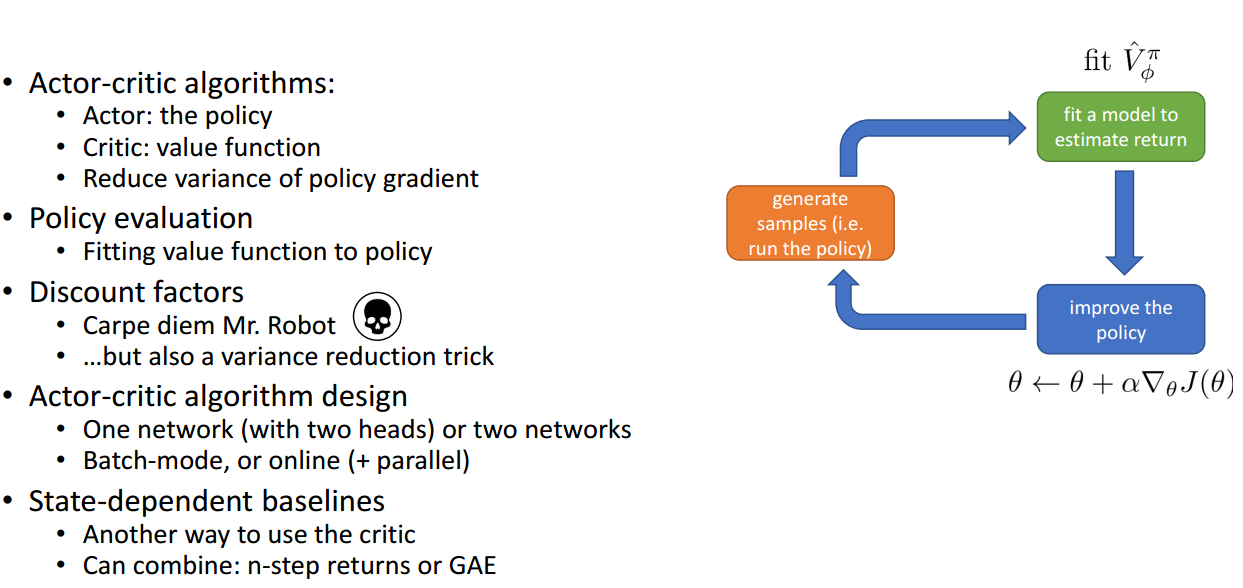
An Actor-Critic Algorithm

Discount Factors for Policy Gradients
针对任务无线episode的情况,V值有可能无线的增大,因此引入了折扣系数,强调现在的reward比将来的reward更重要,权重系数更高:
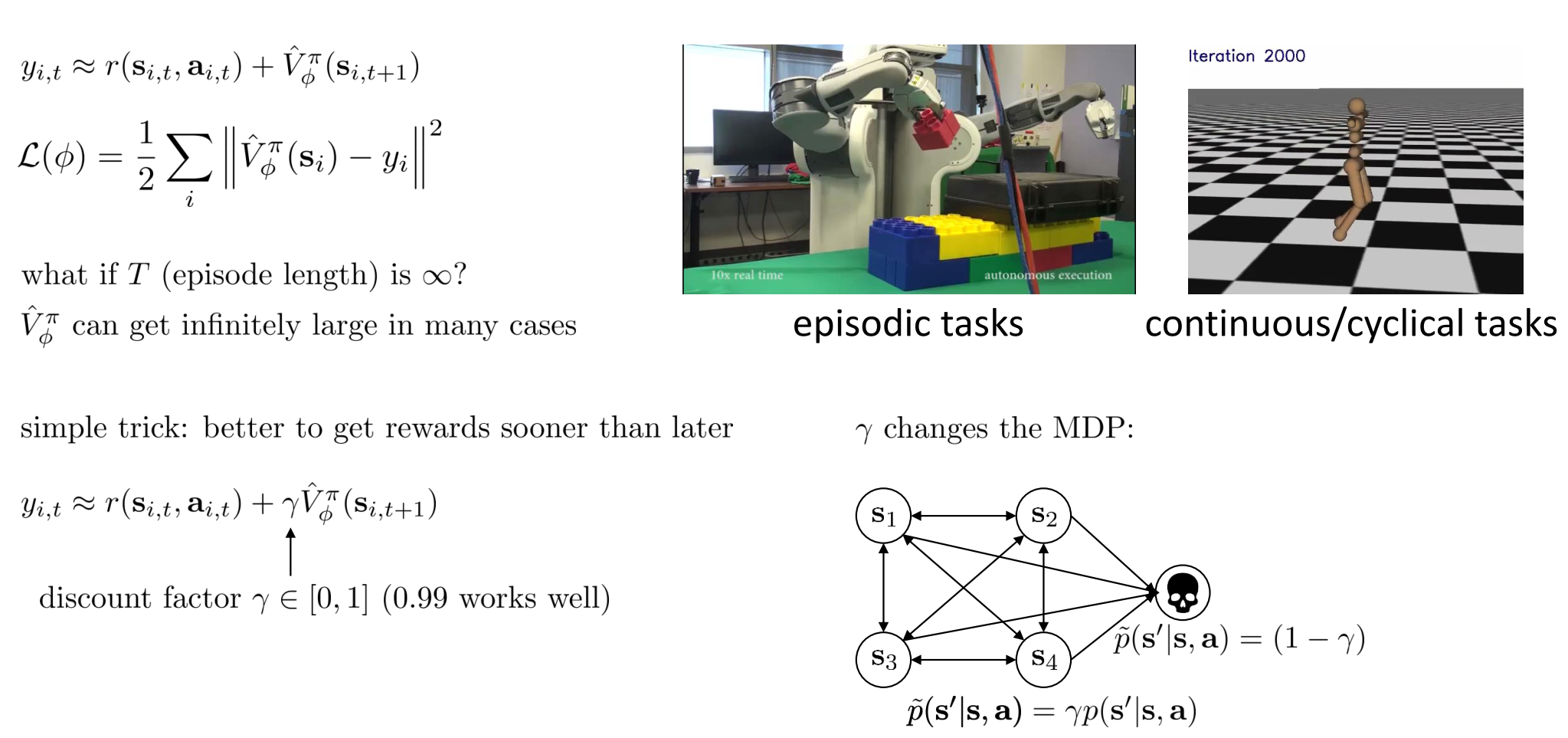

Option 1 is what we actually use.
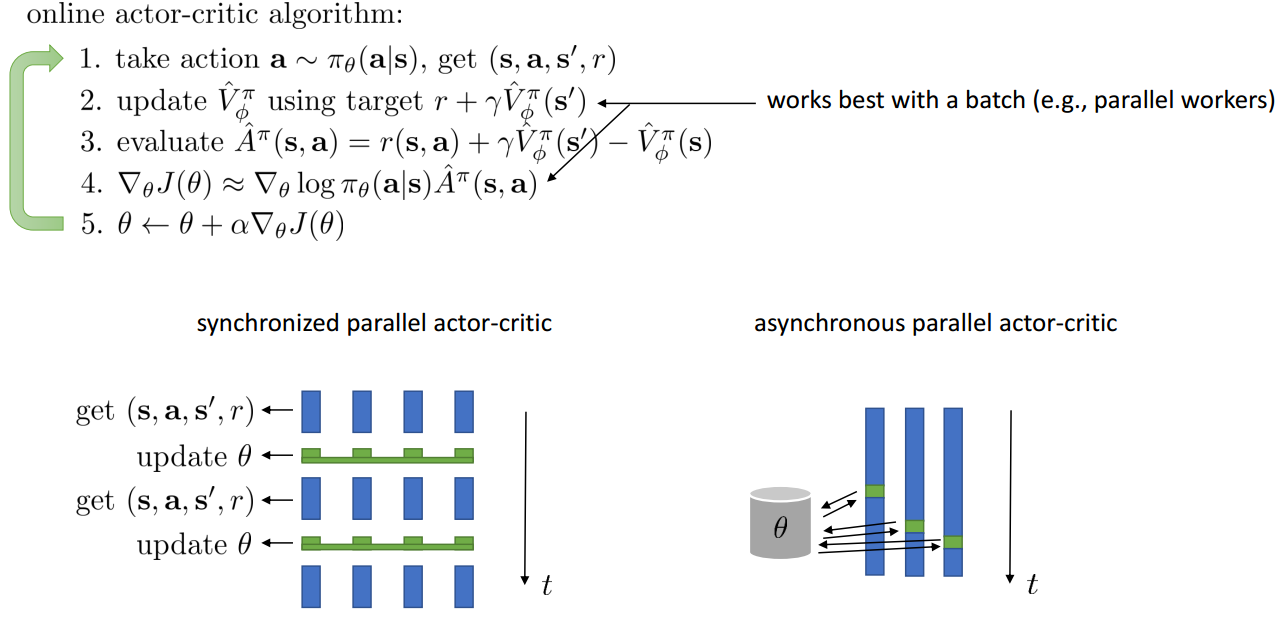
Actor-Critic Algorithms with Discount

注意,通常情况下上面的Online learning方法不会work.需要做网络设计
Architecture Design

Online Actor-Critic in Practice
Critics as State-Dependent Baselines

Eligibility Traces & N-Step Returns

Generalized Advantage Estimation

Review for Policy Gradient
Actor-critic suggested readings
Classic Papers
DRL Actor-Critic Papers
- Mnih (2016). Asynchronous methods for deep reinforcement learning: A3C – parallel online actor-critic
- Schulman (2016). High-dimensional continuous control using generalized advantage estimation: batch-mode actor-critic with blended Monte Carlo and function approximator returns
- Gu (2017). Q-Prop: sample-efficient policy gradient with an off-policy critic: policy gradient with Q-function control variate
Note: Cover Picture
