Terminology & Notation
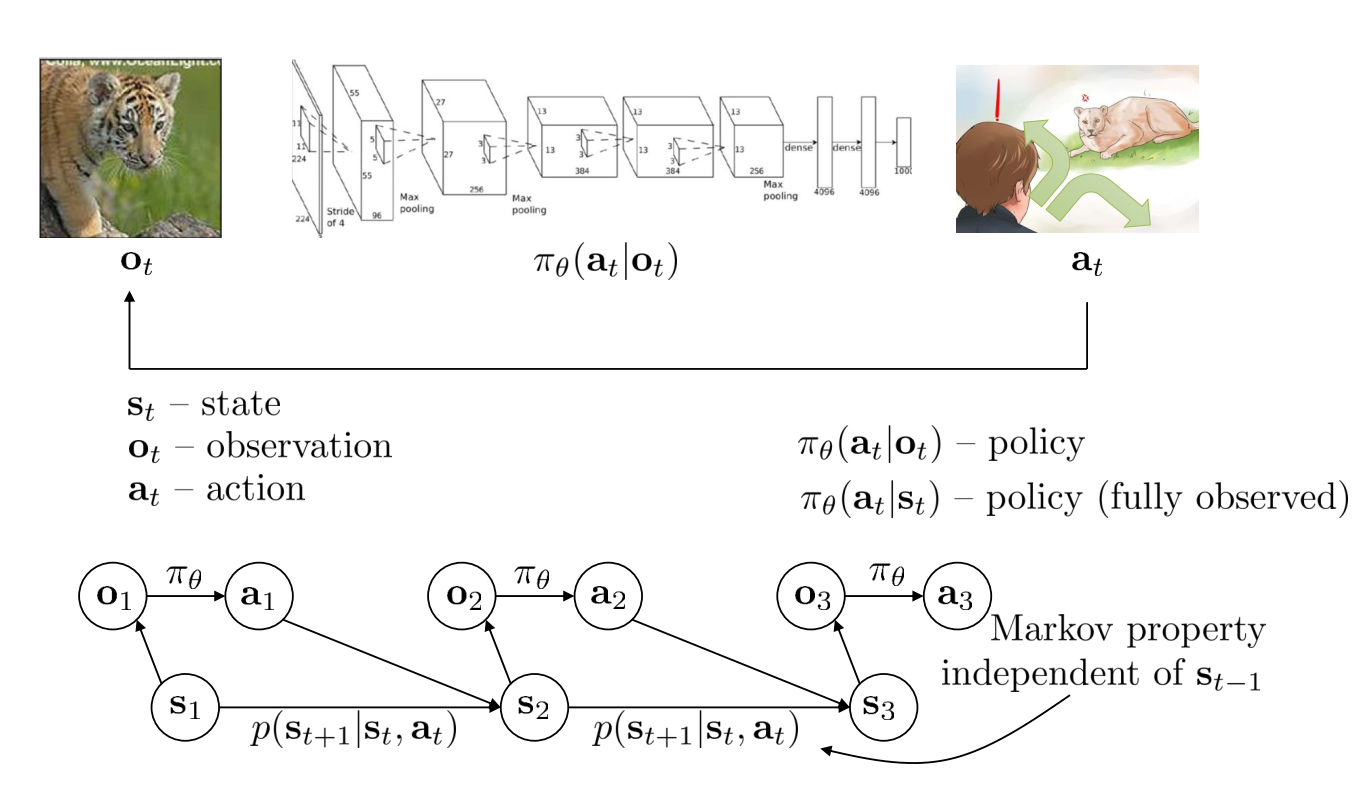
Definitions

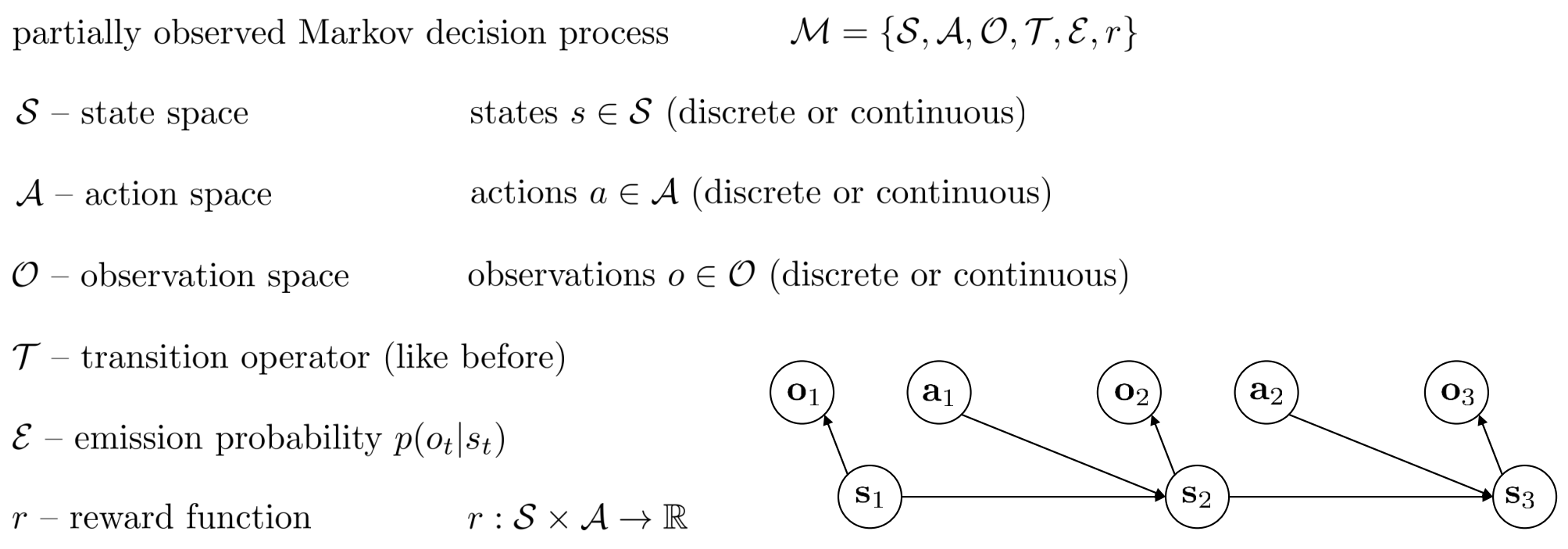
MDP

POMDP
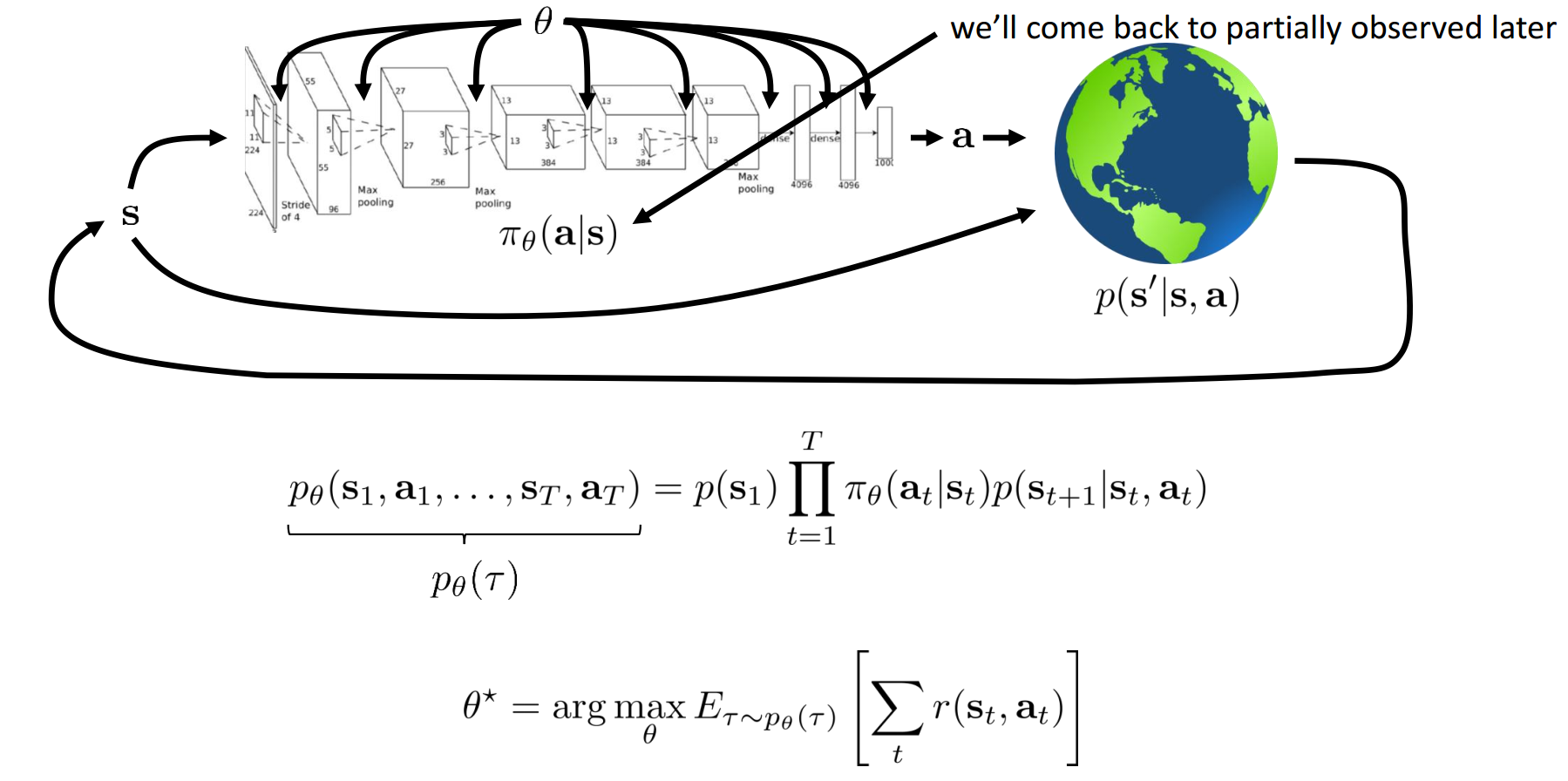
The Goal of Reinforcement Learning
Markov chain on $(s,a)$:
$$ p((s_{t+1}, a_{t+1})| (s_t, a_t)) = p(s_{t+1}|s_t, a_t) \pi_\theta(a_{t+1}|s_{t+1}) $$
Finite Horizon Case: State-action Marginal
$p_\theta(s_t,a_t)$ is state-action marginal.
$$ \theta^* = arg \max_{\theta} E_{\tau \sim p_\theta(\tau)} \left [ \sum_t r(s_t, a_t) \right ] = arg \max_{\theta} \sum_{t=1}^T E_{(s_t,a_t) \sim p_{\theta}(s_t,a_t) } \left [ r(s_t, a_t) \right ] $$
Infinite Horizon Case: Stationary Distribution

Expectations and Stochastic Systems
For infinite horizon case:
$$ \theta^* = arg \max_\theta E_{(s,a) \sim p_\theta(s,a)} \left [r(s,a) \right] $$
For finite horizon case:
$$ \theta^* = arg \max_\theta \sum_{t=1}^T E_{(s_t,a_t) \sim p_\theta(s_t,a_t)} \left [r(s_t,a_t) \right ] $$
In RL, we almost always care about expectations.
- $r(x)$ -> not smooth
- $\pi_\theta(a=fall) = \theta$
- $E_{\pi_\theta}\left [ r(x) \right]$ -> smooth in $\theta$!
RL Algorithms
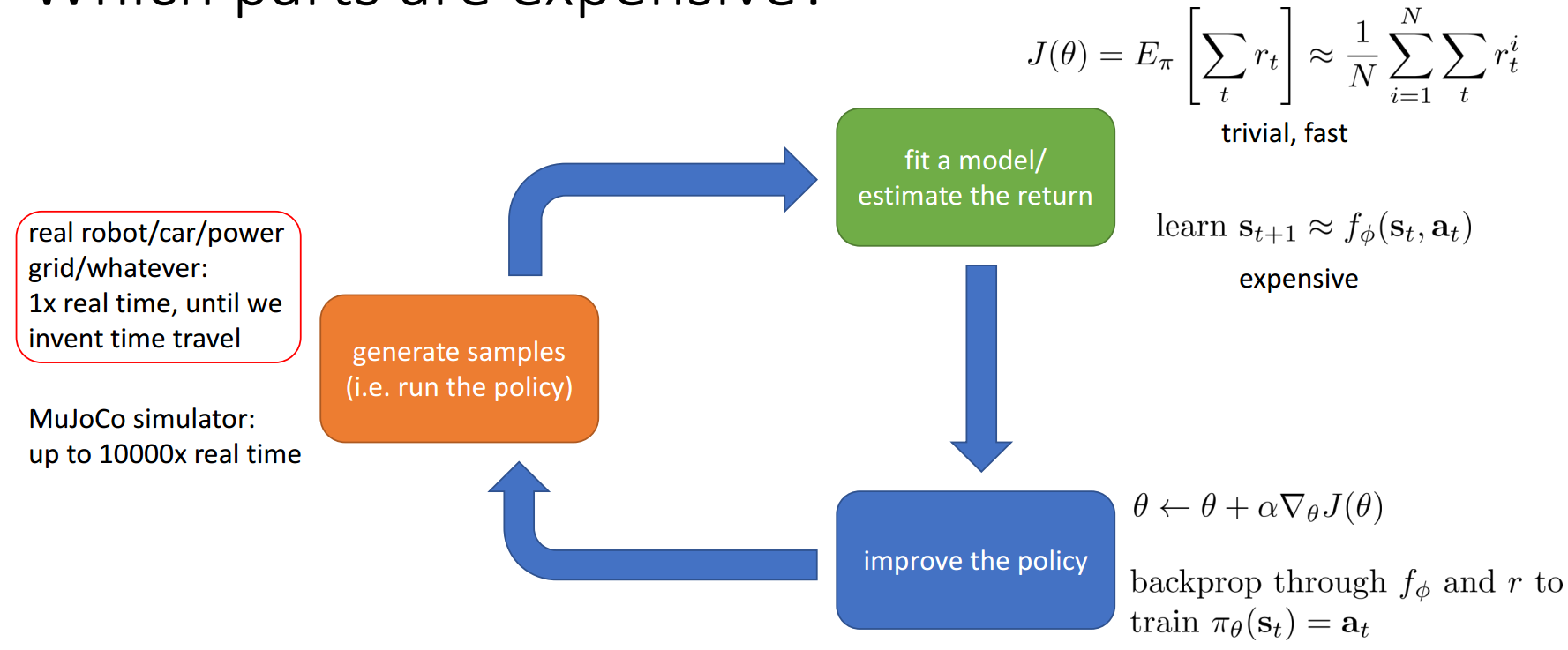
Structure of RL Algorithms
- Sample generation
- Fitting a model/estimating return
- Policy improvement
The Anatomy of a RL Algorithm
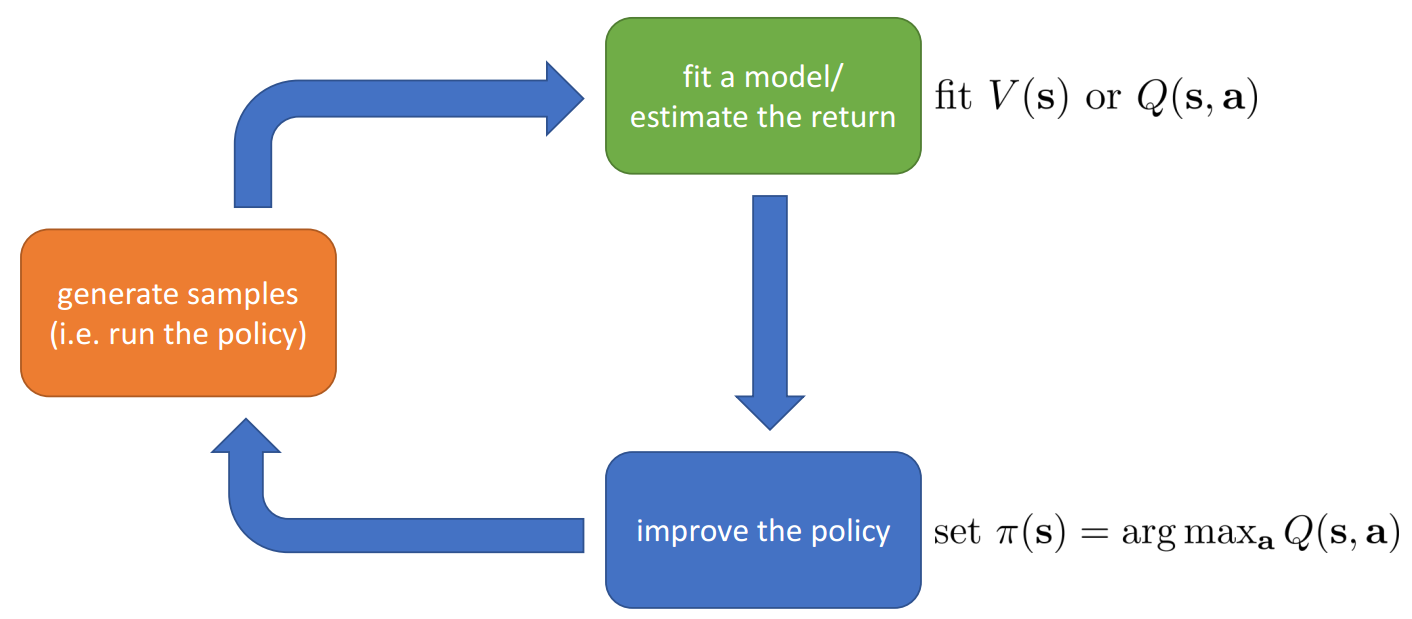
Q-Function
Q-function is the total reward from taking $a_t$ in $s_t$:
$$ Q^{\pi}(s_t,a_t) = \sum_{t\prime = t}^T E_{\pi_\theta} \left[ r( s_t\prime, a_t\prime ) | s_t, a_t \right ] $$
Value-Function
Value-function is the total reward from $s_t$:
$$ V^\pi(s_t) = \sum_{t\prime = t}^T E_{\pi_\theta} \left [ r(s_{t\prime},a_{t\prime} ) | s_t \right ] $$
$$ V^\pi(s_t) = E_{a_t \sim \pi(a_t|s_t)} \left [ Q^\pi(s_t, a_t) \right ] $$
$E_{s_1 \sim p(s_1)} \left [ V^\pi(s_t) \right ]$ is the RL objective!
Using Q-Function and Valuer Functions

Types fo RL Algorithms
The goal of RL:
$$ \theta^* = arg \max_{\theta} E_{\tau \sim p_\theta(\tau)} \left [ \sum_t r(s_t, a_t) \right ] $$
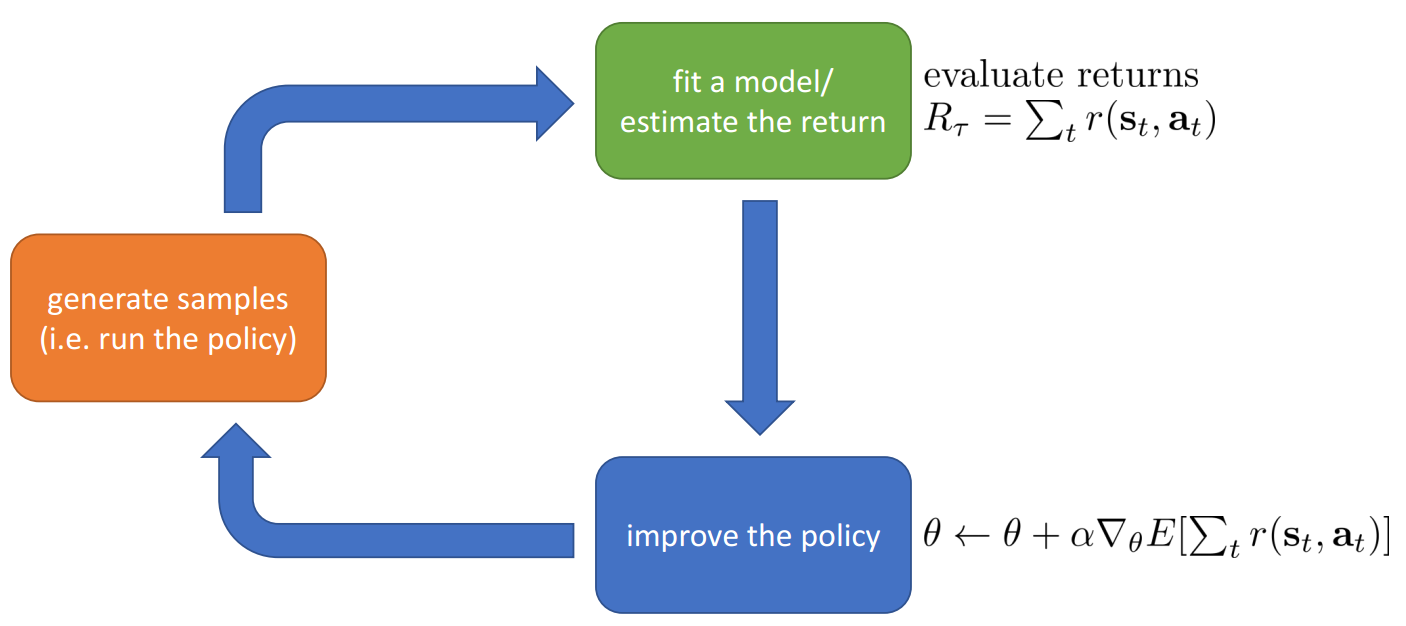
- Policy gradients: directly differentiate the above objective
- Value-based: estimate value function or Q-function of the optimal policy (no explicit policy)
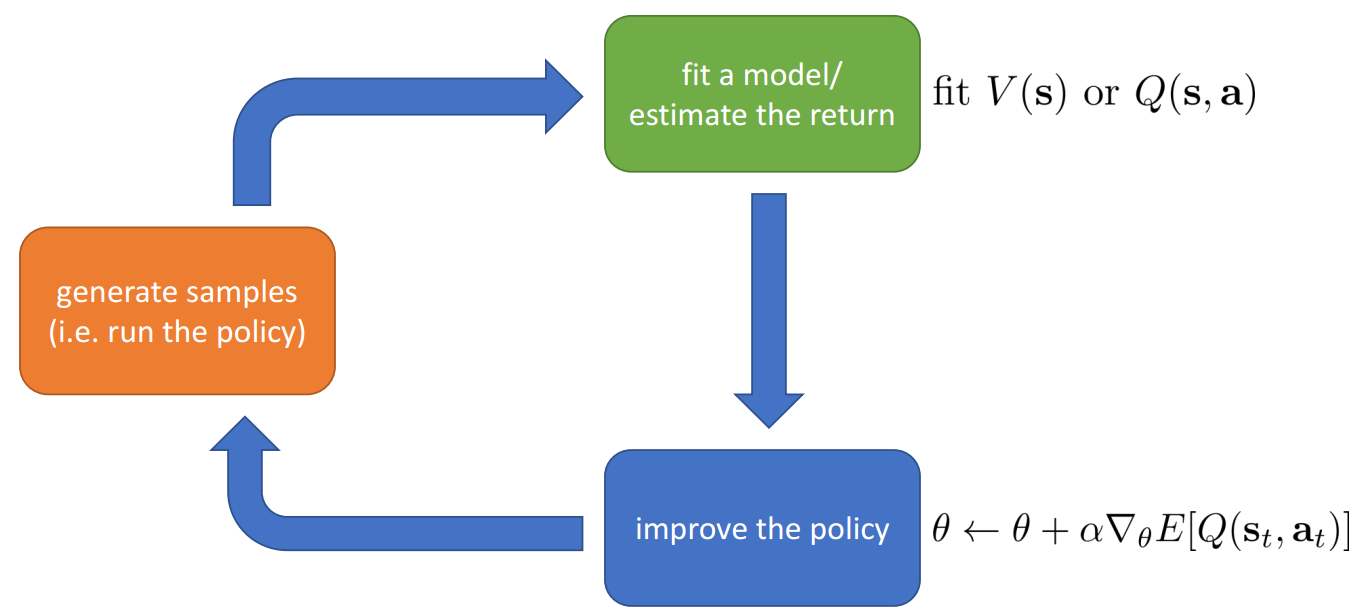
- Actor-critic: estimate value function or Q-function of the current policy, use it to improve policy
- Model-based RL: estimate the transition model, then improve the policy
Model-based RL
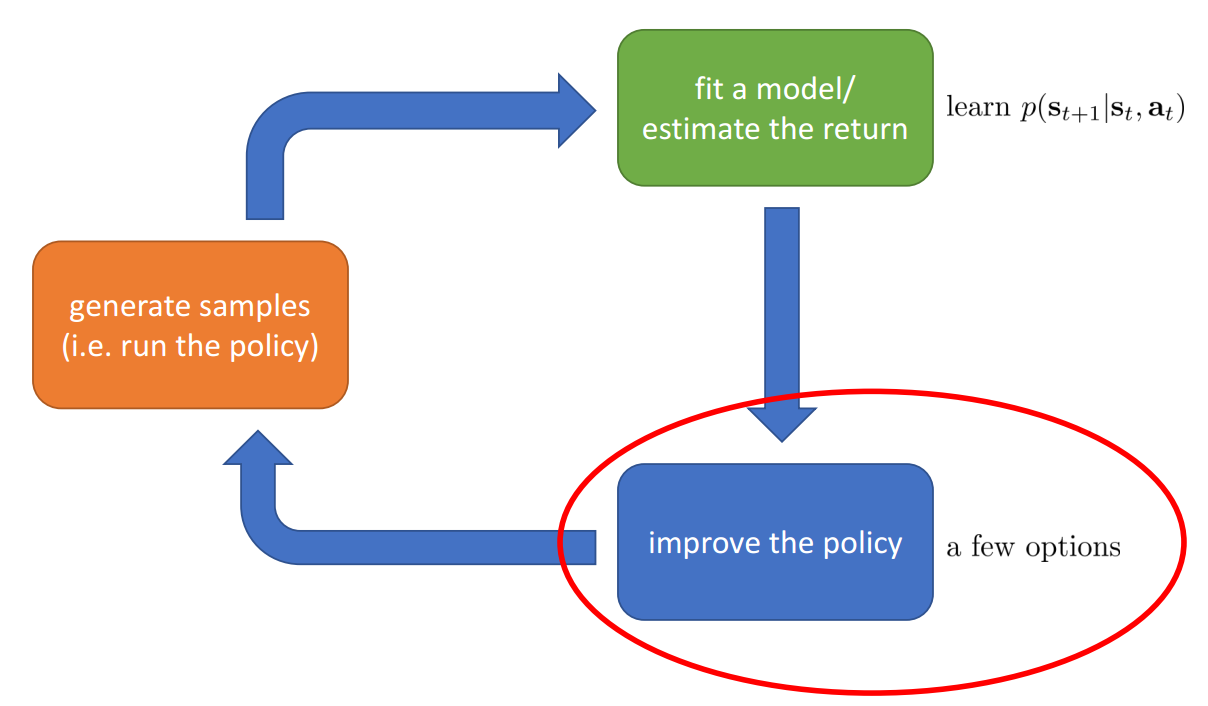
Estimate the transition model, then improve the policy by:
- Just use the model to plan (no policy)
- Trajectory optimization/optimal control (primarily in continuous spaces) – essentially back-propagation to optimize over actions
- Discrete planning in discrete action spaces – e.g., Monte Carlo tree search
- Back-propagate gradients into the policy
- Requires some tricks to make it work
- Use the model to learn a value function
- Dynamic programming
- Generate simulated experience for model-free learner
Value-Function based RL
Direct Policy Gradients
Actor-Critic: Value Functions + Policy Gradients
Why So Many RL Algorithms
- Different tradeoffs
- Sample efficiency
- Stability & ease of use
- Different assumptions
- Stochastic or deterministic?
- Continuous or discrete?
- Episodic or infinite horizon?
- Different things are easy or hard in different settings
- Easier to represent the policy?
- Easier to represent the model?
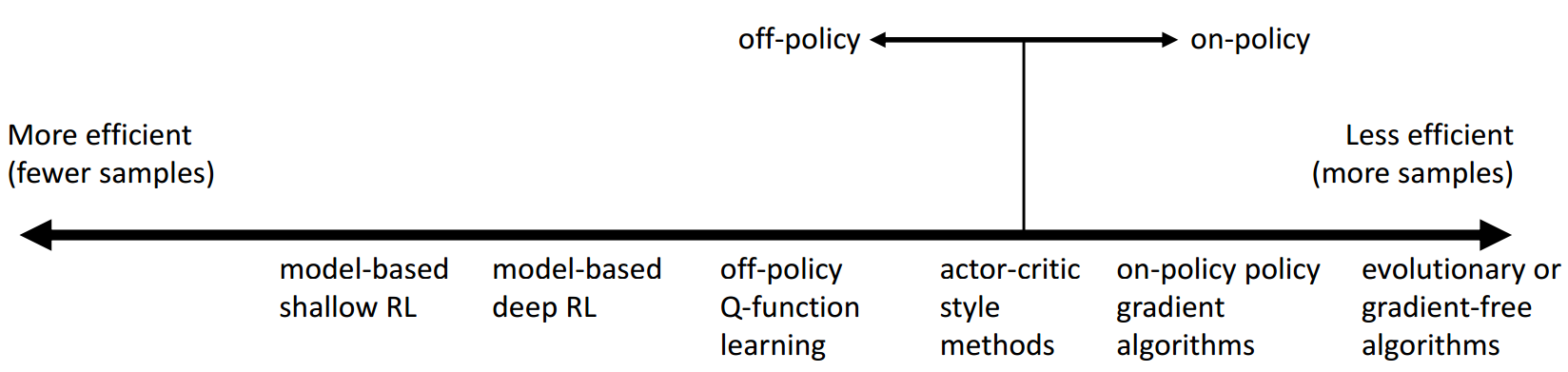
Comparison: Sample Efficiency
Sample efficiency: how many samples do we need to get a good policy?
Most important question: is the algorithm off policy?
- Off policy: able to improve the policy without generating new samples from that policy
- On policy: each time the policy is changed, even a little bit, we need to generate new samples
Comparison: Stability and Ease of Use
Question:
- Does it converge?
- And if it converges, to what?
And does it converge every time?
Supervised learning: almost always gradient descent
Reinforcement learning: often not gradient descent
- Q-learning: fixed point iteration
- At best, minimizes error of fit (“Bellman error”)
- Not the same as expected reward
- At worst, doesn’t optimize anything
- Many popular deep RL value fitting algorithms are not guaranteed to converge to anything in the nonlinear case
- At best, minimizes error of fit (“Bellman error”)
- Model-based RL: model is not optimized for expected reward
- Model minimizes error of fit
- This will converge
- No guarantee that better model = better policy
- Policy gradient
- The only one that actually performs gradient descent(ascent) on the true objective, but also often the least efficient!
- Q-learning: fixed point iteration
Comparison: Assumptions
- Common assumption #1: full observability
- Generally assumed by value function fitting methods
- Can be mitigated by adding recurrence
- Common assumption #2: episodic learning
- Often assumed by pure policy gradient methods
- Assumed by some model-based RL methods
- Common assumption #3: continuity or smoothness
- Assumed by some continuous value function learning methods
- Often assumed by some model-based RL methods
Examples of Specific Algorithms
- Value function fitting methods
- Q-learning, DQN
- Temporal difference learning
- Fitted value iteration
- Policy gradient methods
- REINFORCE
- Natural policy gradient
- Trust region policy optimization
- Actor-critic algorithms
- Asynchronous advantage actor-critic (A3C)
- Soft actor-critic (SAC)
- Model-based RL algorithms
- Dyna
- Guided policy search
Note: Cover Picture
