Policy Gradients
See more from this blog
Partial Observability
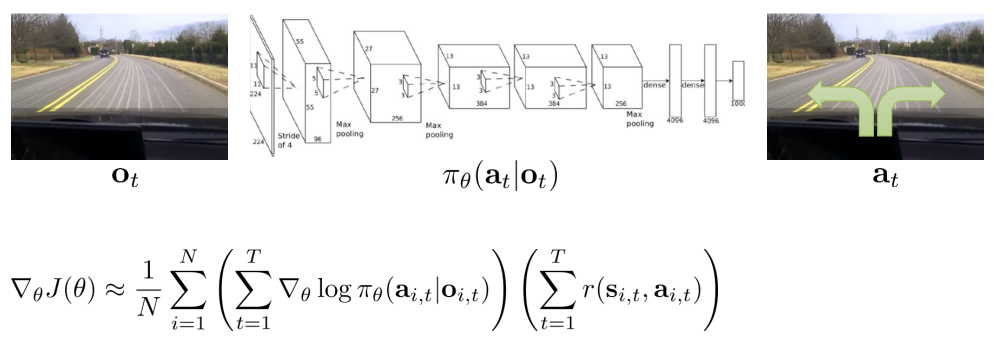
Markov property is not actually used!
Can use policy gradient in partially observed MDPs without modification.
What is Wrong with the Policy Gradient
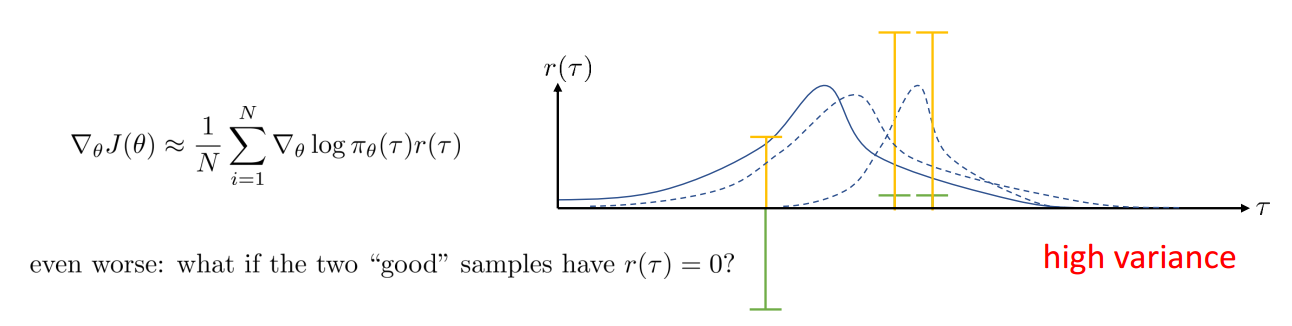
策略梯度法存在的一个问题是有较大的方差。
在强化学习中，存在一个因果关系，即现在时刻的策略不能影响过去时刻策略的reward情况： policy at time t’ cannot affect reward at time t when t < t’.
Baselines
Subtracting a baseline is unbiased in expectation!
Average reward is not the best baseline, but it’s pretty good!
Analyzing Variance
Section Review
- The high variance of policy gradient
- Exploiting causality
- Future doesn’t affect the past
- Baselines
- Unbiased
- Analyzing variance
- Can derive optimal baselines
Policy Gradient is On-policy
对于梯度策略方法来说，最大的问题是：
梯度策略是on-policy的，但是在优化时需要针对当前的策略采样轨迹，一点点的神经网络参数修改都会导致策略的不同，因此on-policy学习是及其不高效的。
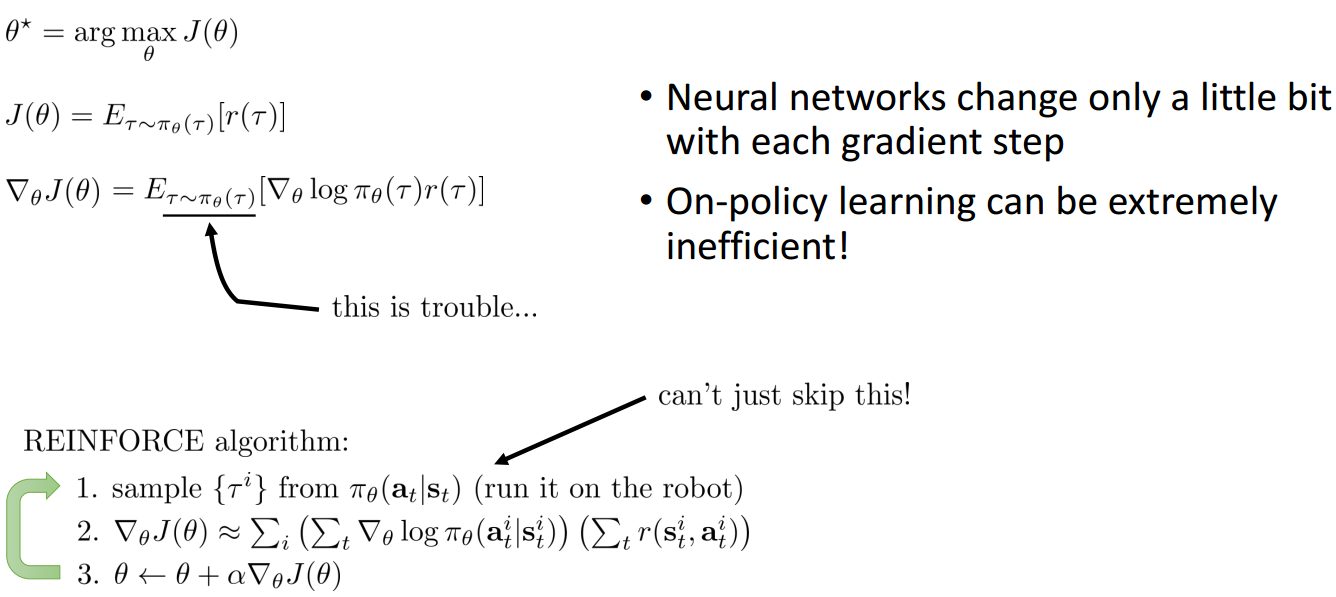
Off-policy Learning & Importance Sampling
解决该问题的方法就是使用重要性采样，其核心就是将原本属于难采集数据分布$\pi_\theta(\tau)$的样本$x$，
变相为从另一个易采集数据分布$\bar{\pi}_\theta(\tau)$的样本$x\prime$
下图中最后一个公式很重要，在后面会进行替换。
Deriving the Policy Gradient with IS
The Off-Policy Policy Gradient
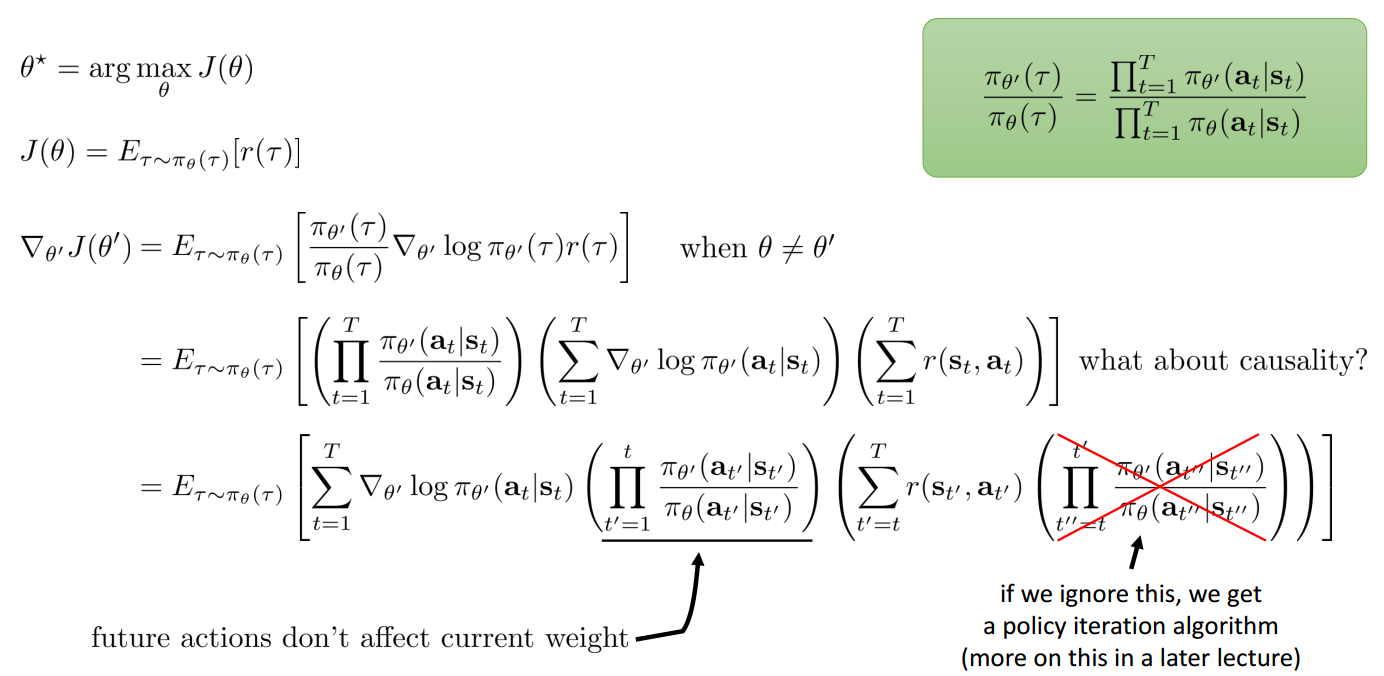
A first-order Approximation for IS
Policy Gradient with Automatic Differentiation
Pseudo-code example (with discrete actions):
Maximum likelihood
# Given:
# actions - (N*T) x Da tensor of actions
# states - (N*T) x Ds tensor of states
# Build the graph:
logits = policy.predictions(states) # This should return (N*T) x Da tensor of action logits
negative_likelihoods = tf.nn.softmax_cross_entropy_with_logits(labels=actions, logits=logits)
loss = tf.reduce_mean(negative_likelihoods)
gradients = loss.gradients(loss, variables)
Policy Gradient
# Given:
# actions - (N*T) x Da tensor of actions
# states - (N*T) x Ds tensor of states
# q_values – (N*T) x 1 tensor of estimated state-action values
# Build the graph:
logits = policy.predictions(states) # This should return (N*T) x Da tensor of action logits
negative_likelihoods = tf.nn.softmax_cross_entropy_with_logits(labels=actions, logits=logits)
weighted_negative_likelihoods = tf.multiply(negative_likelihoods, q_values)
loss = tf.reduce_mean(weighted_negative_likelihoods)
gradients = loss.gradients(loss, variables)
$$ \bar{J(\theta)} \approx \frac{1}{N}\sum_{i=1}^{N} \sum_{t=1}^{T} \log \pi_\theta(a_{i,t} | s_{i,t}) Q_{i,t} $$
在最后乘以期望的reward之和及为Q值。
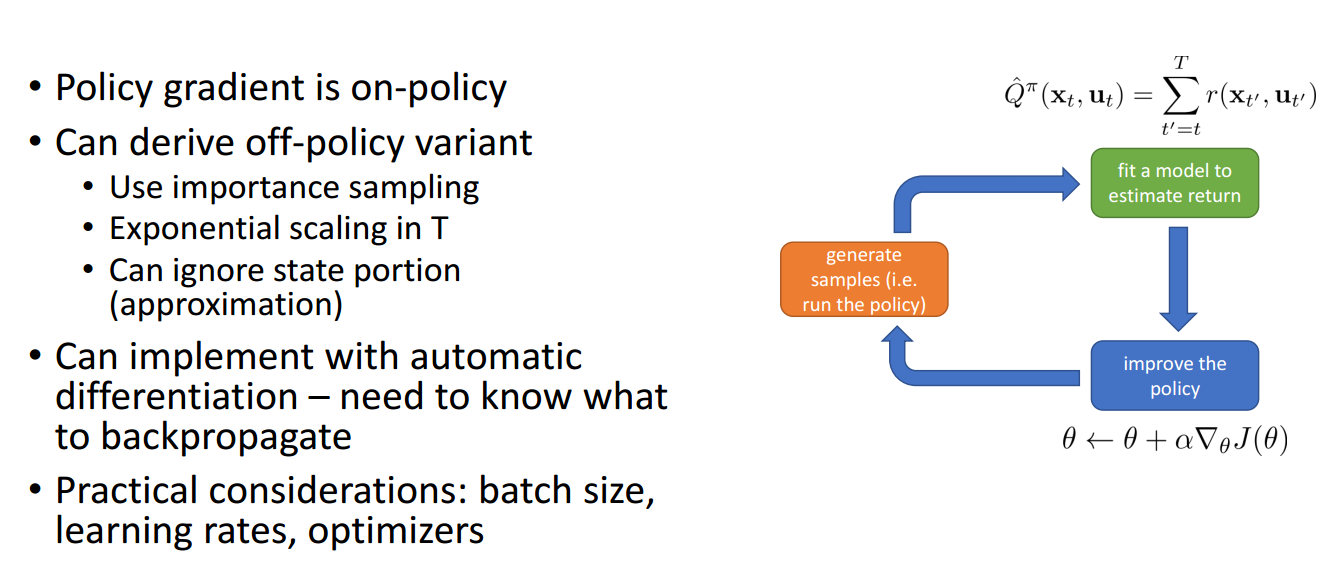
Policy Gradient in Practice
Remember that the gradient has high variance - This isn’t the same as supervised learning! - Gradients will be really noisy! - Consider using much larger batches - Tweaking learning rates is very hard - Adaptive step size rules like ADAM can be OK-ish
Section Review
Covariant/Natural Policy Gradient
简单的策略梯度存在的问题是有些参数改变的可能性要比其他参数大
TRPO
Trust region policy optimization: deep RL with natural policy gradient and adaptive step size.
Policy Gradient Suggested Readings
Classic Papers
- Williams (1992). Simple statistical gradient-following algorithms for connectionist reinforcement learning: introduces REINFORCE algorithm
- Baxter & Bartlett (2001). Infinite-horizon policy-gradient estimation: temporally decomposed policy gradient
- Peters & Schaal (2008). Reinforcement learning of motor skills with policy gradients: very accessible overview of optimal baselines and natural gradient
DRL Policy Gradient Papers
- Levine & Koltun (2013). Guided policy search: deep RL with importance sampled policy gradient
- Schulman, L., Moritz, Jordan, Abbeel (2015). Trust region policy optimization: deep RL with natural policy gradient and adaptive step size
- Schulman, Wolski, Dhariwal, Radford, Klimov (2017). Proximal policy optimization algorithms: deep RL with importance sampled policy gradient
Note: Cover Picture