Unsupervised Learning
- Dimension Reduction
- Preprocessing: Huge dimension, say 224*224, is hard to process
- Visualization: Tensorflow Projector
- Taking advantage of unsupervised data
- Compression, denoising, super-resolution…
Auto-Encoders
详见Code
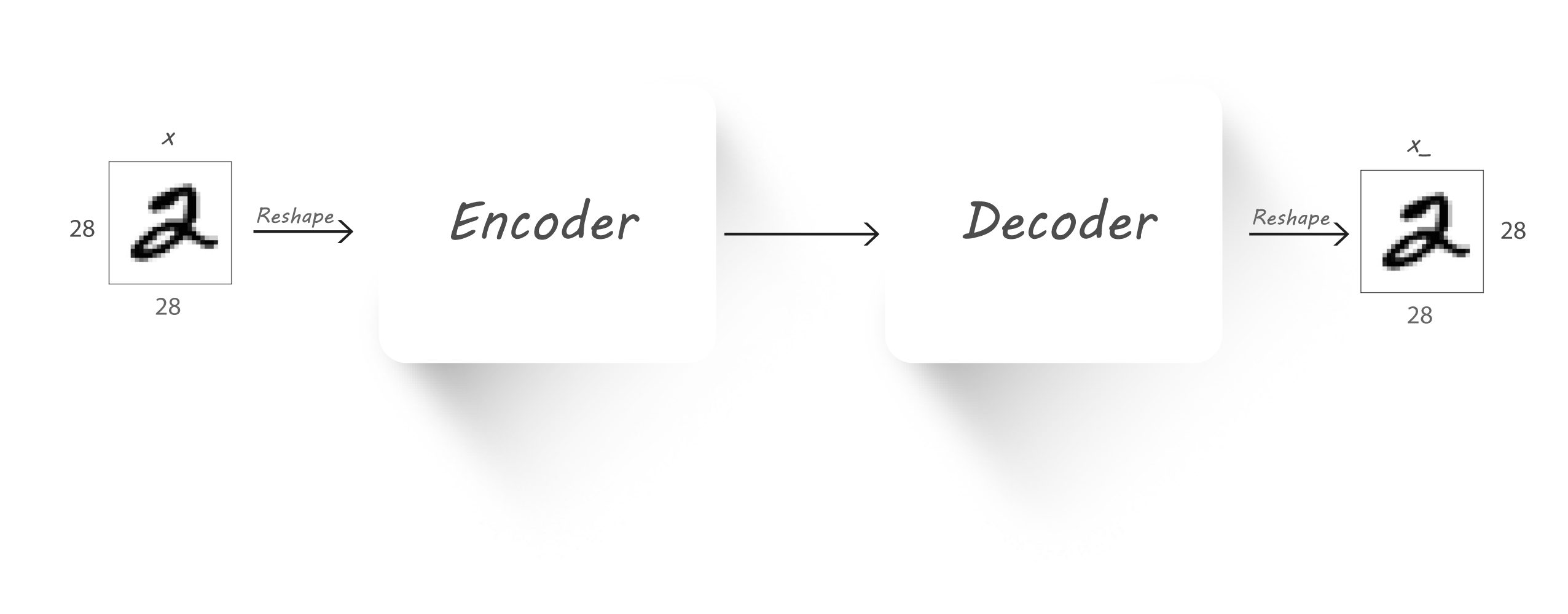
How to Train
Loss function for binary inputs
$$ l(f(x)) = - \sum_{k} (x_k \log(\hat{x}_k) + (1 - x_k) \log(1-\hat{x}_k)) $$
- Cross-entropy error function (reconstruction loss) $f(x) \equiv \hat{x}$
- Cross-entropy error function (reconstruction loss) $f(x) \equiv \hat{x}$
Loss function for real-valued inputs
$$ l(f(x)) = \frac{1}{2} \sum_k (\hat{x}_k - x_k)^2 $$
- Sum of squared differences(reconstruction loss)
- We use a linear activation function at the output
PCA vs AUto-Encoders
PCA在高维数据中找到最大方差的方向,仅选择那些方差最大的轴;但是,PCA的线性度对可提取的特征维的种类产生了重大限制。
Denoising Auto-Encoders
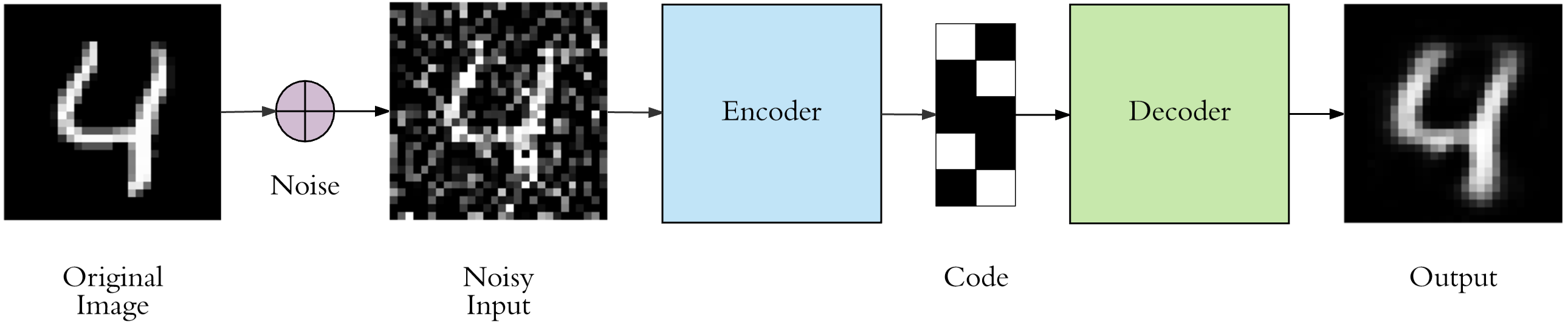
Adversarial Auto-Encoders
在训练Auto-Encoder的时候,Latent vector z的分布不均匀,会导致恢复的图片效果不好。有多种方法解决该问题:
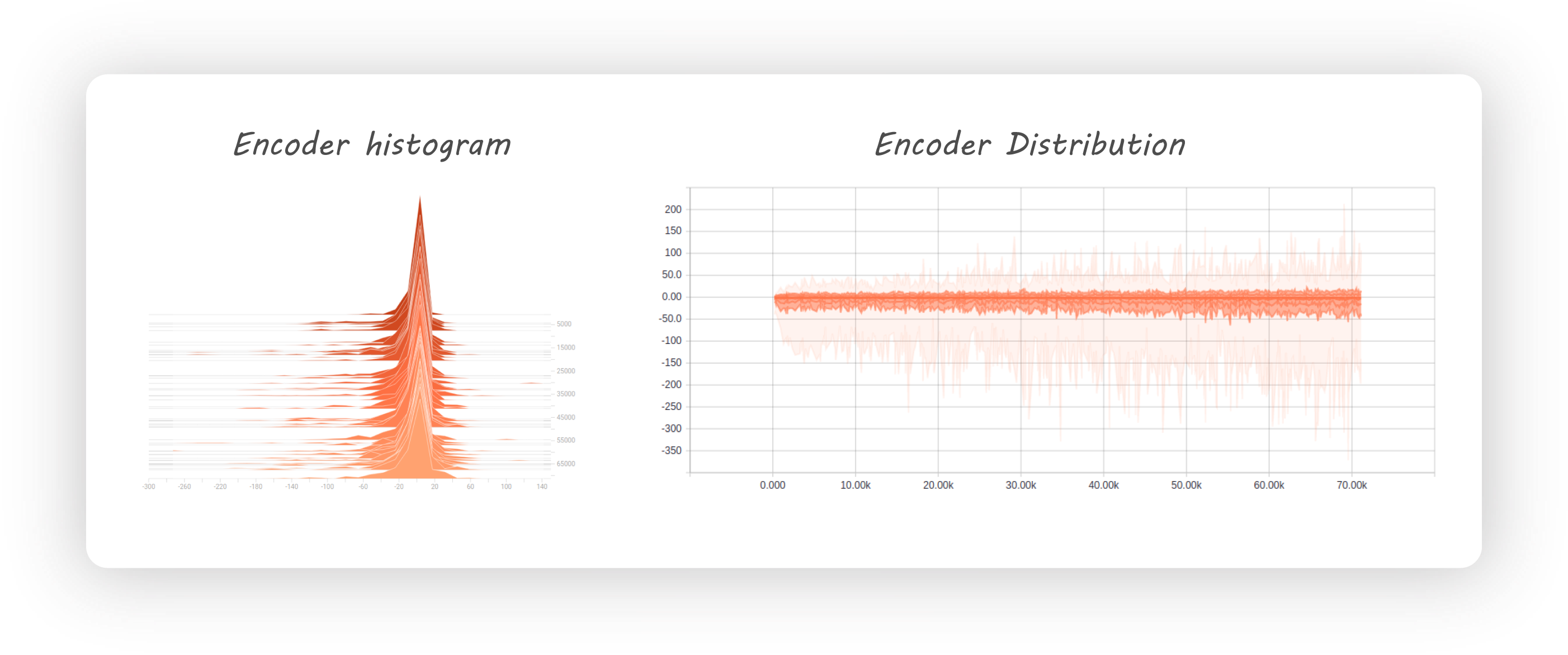
通过添加一个辨别器,强制训练该Encoder网络,让其输出z的分布达到期望的分布,如N(0,1)。
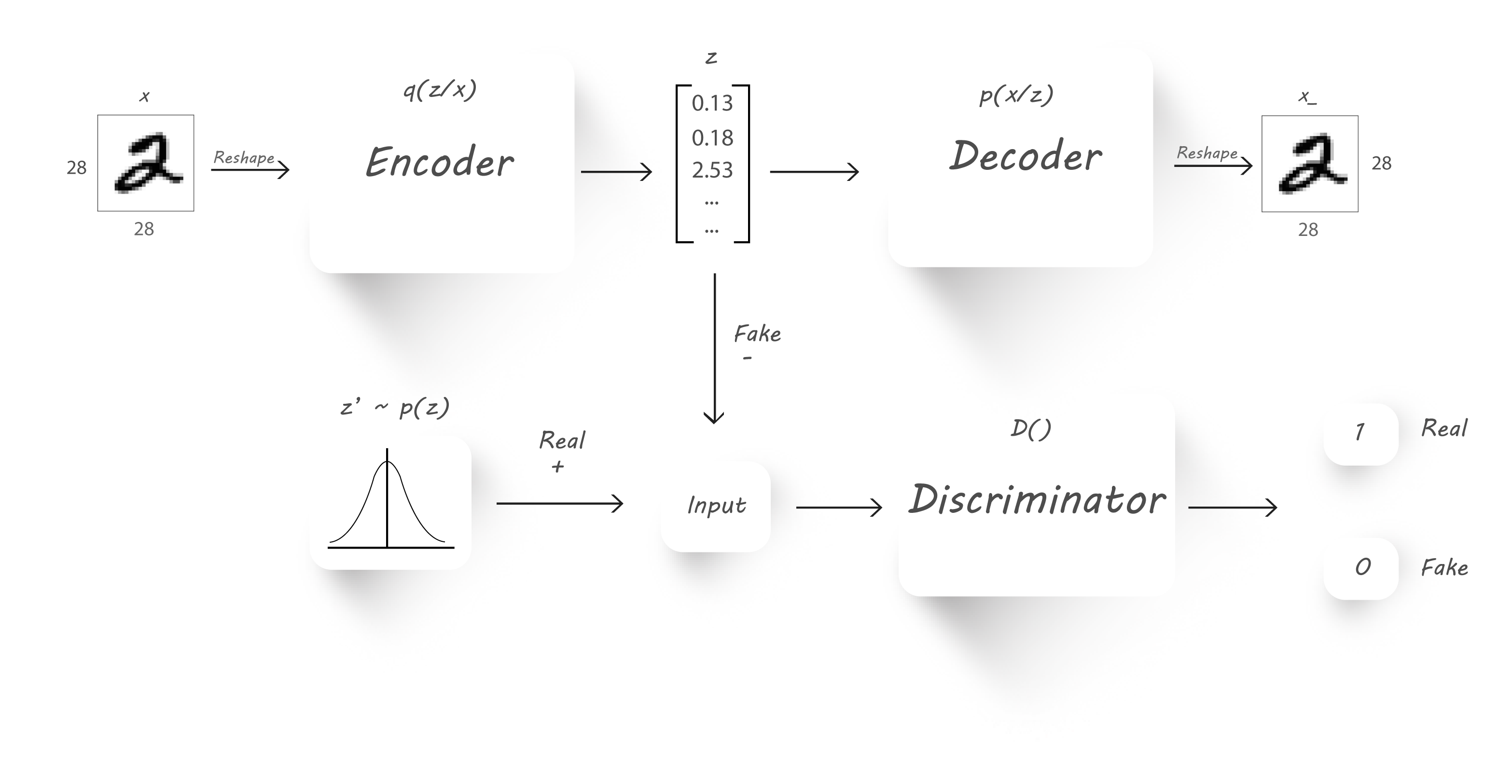
Variational Auto-Encoders
Loss Function
损失函数由两部分组成,第一部分是确保Decoder网络能够从Latent vector z中复原x, 即上面how to train中的损失函数,最大化其概率即最小化其负数,KL散度是一个正则化惩罚项,p我们可以提前假设为是一个正态分布,训练q越接近p越好,因此是最小化KL散度。
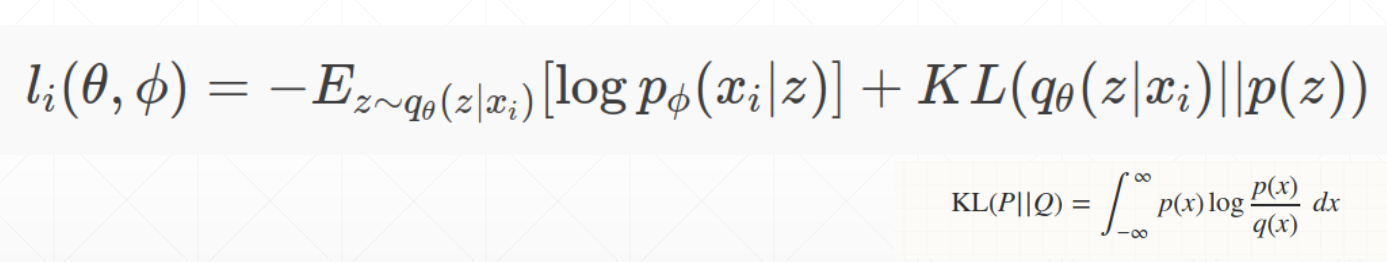
每部分的效果:
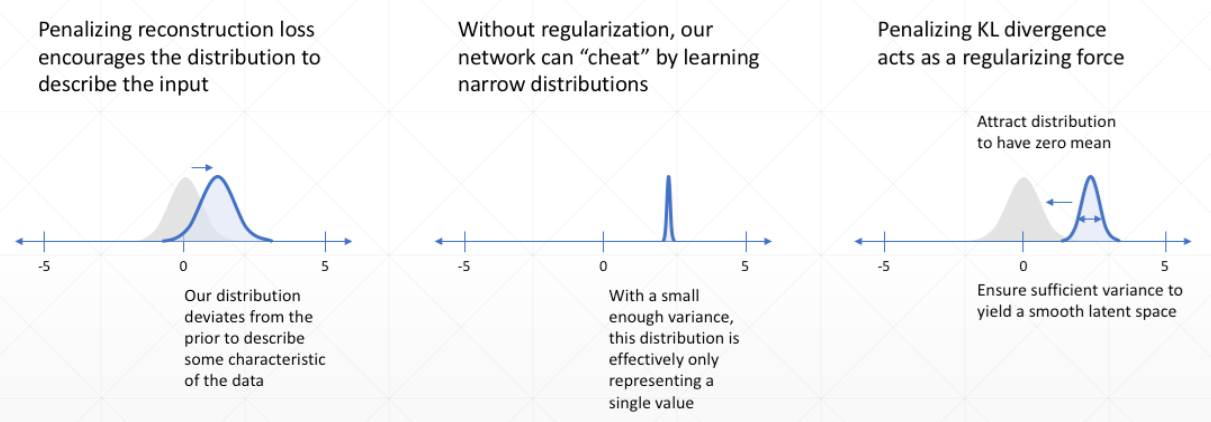
如何最小化两个分布的散度:
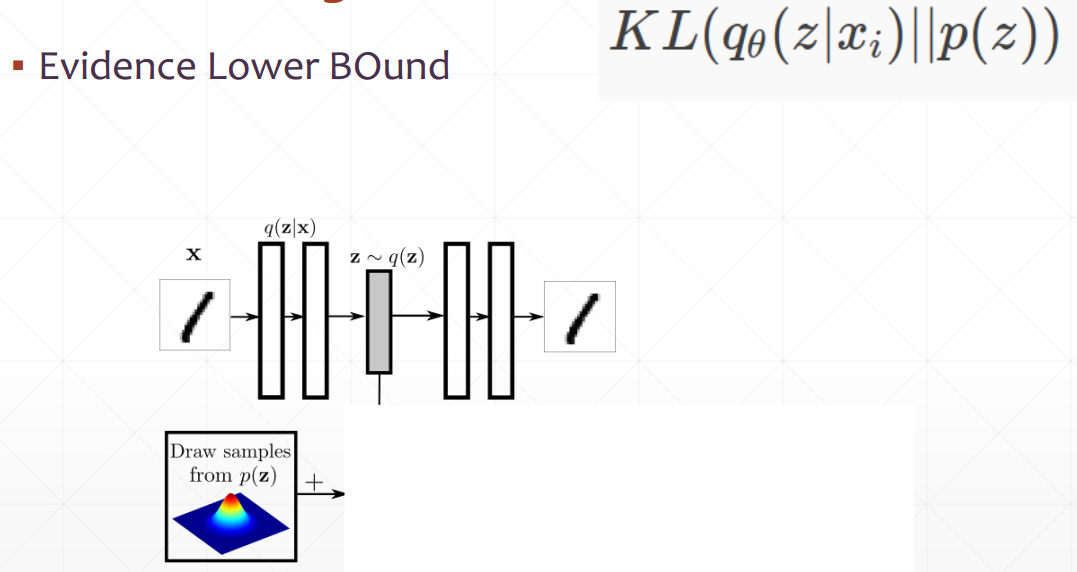
如果两个分布都是正态分布,则两个分布的散度计算公式为:
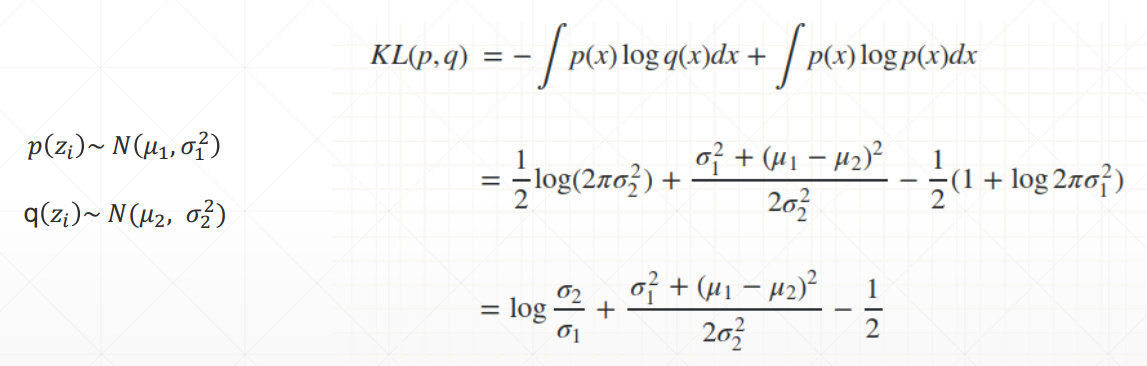
VAE的Encoder输出是两个参数,描述的是x的分布,因此需要从该分布中sample出来z向量提供给Decoder复原x,但是sample操作是不可微分的,所以VAE作者提出一个reparameterization trick,并不是从分布中采样,而是利用公式$z = \mu + \sigma \odot \epsilon$直接得到向量z,具体描述如下图:
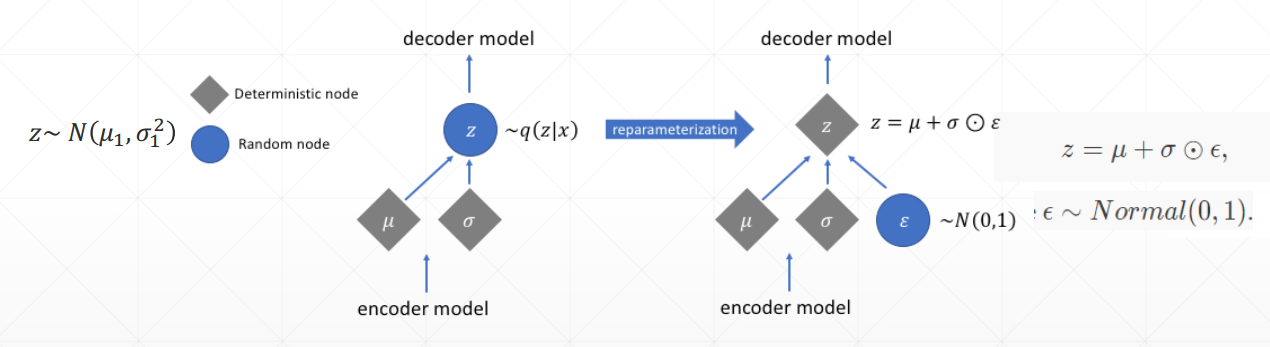
这样方向传播误差的时候,可以抛弃掉$\epsilon$的部分影响,可以对Encoder进行微分:
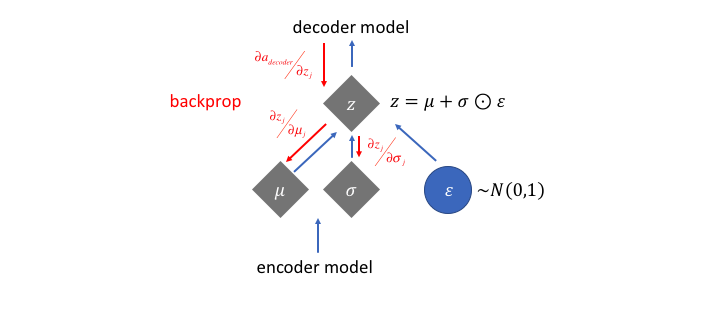
从神经网络结构的角度看:
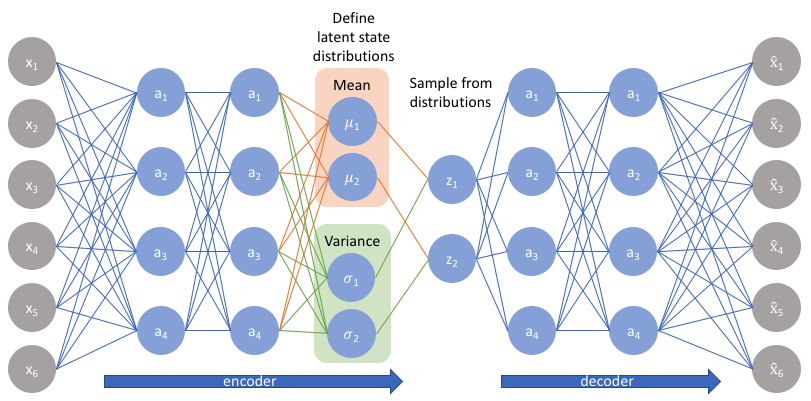
VAE是Generative Model:
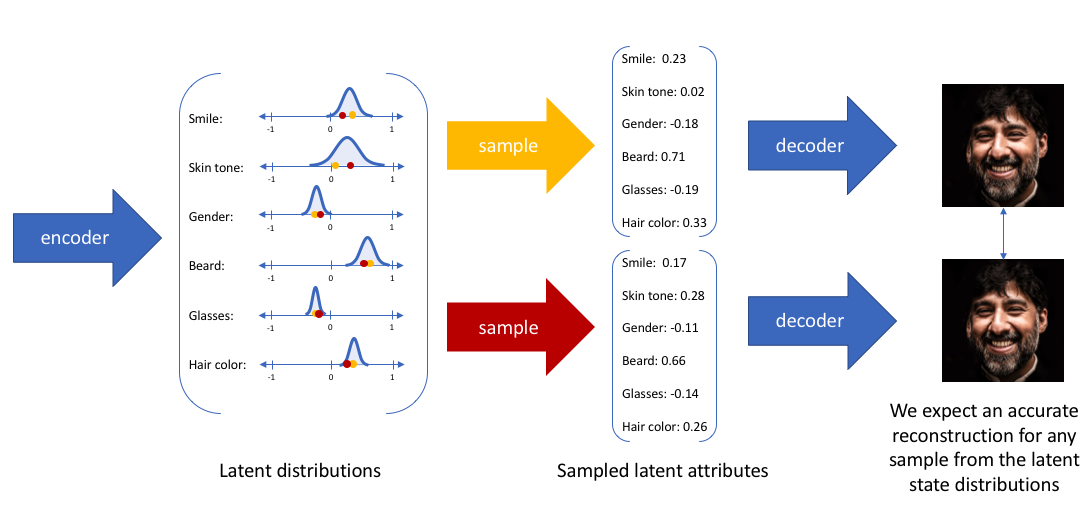
Reference
Note: Cover Picture
